Производные основных элементарных функций и их вывод

Представлены производные основных элементарных функций и ссылки на страницы с их выводом. Даны формулы производных высших порядков.

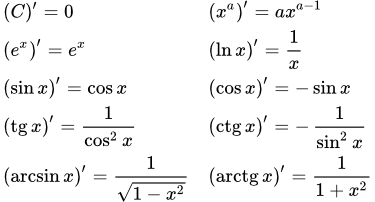
Производная логарифма

( ln x )^′ = 1x;     ( ln | x |  )^′ = 1x;
( log_a x )^′ = ( ln xln a )^′ = 1x ln a;     ( log_a | x |  )^′ = 1x ln a.
См. Вывод производной логарифма тремя способами >>>

Производная степенной и показательной функций

( x^a )^′ = ax^a – 1;
( ⁿ√ x^m  )^′ = ( x^m / n )^′ = mn x^mn – 1 = mn ⁿ√ x^m – n ;
См. Вывод производной степенной функции >>>

( e^x )^′ = e^x;
( a^x )^′ = ( e^{(ln a) ⋅ x} )^′ = a^x ⋅ ln a;
См. Вывод производной показательной функции и экспоненты тремя способами >>>

Производные тригонометрических функций

( sin x )^′ = cos x;
См. Вывод производной синуса >>>

( cos x )^′ = –sin x;
См. Вывод производной косинуса >>>

( tg x )^′ = 1cos² x;
См. Вывод производной тангенса >>>

( ctg x )^′ = – 1sin² x;
См. Вывод производной котангенса >>>

Производные обратных тригонометрических функций

( arcsin x )^′ = 1√ 1 – x² ;
( arccos x )^′ = (  π2 – arcsin x )^′ = – 1√ 1 – x² ;
См. Вывод производных арксинуса и арккосинуса двумя способами >>>

( arctg x )^′ = 11 + x²;
( arcctg x )^′ = (  π2 – arctg x )^′ = – 11 + x²;
См. Вывод производных арктангенса и арккотангенса двумя способами >>>

Производные гиперболических функций

( sh x )^′ = ch x;
( ch x )^′ = sh x;
( th x )^′ = 1ch² x;
( cth x )^′ = – 1sh² x;

Производные обратных гиперболических функций

( arsh x )^′ = ( ln( x + √ x² + 1  ) )^′ = 1√ x² + 1 ;
( arch x )^′ = ( ln( x + √ x² – 1  ) )^′ = 1√ x² – 1 ;
( arth x )^′ = (  12 ln 1 + x1 – x  )^′ = 11 – x²;
( arcth x )^′ = (  12 ln x + 1x – 1  )^′ = 11 – x².

Обратный гиперболический косинус является многозначной функцией. Он имеет две ветви:
arch x = ln( x + √ x² – 1  )  – главное значение;
arch x = –ln( x + √ x² – 1  ) = ln( x – √ x² – 1  ).
Иногда значения для двух ветвей пишут одной формулой:
arch x = ln( x ± √ x² – 1  ).
Тогда его производная имеет вид:
( arch x )^′ = ( ln( x ± √ x² – 1  ) )^′ = ± 1√ x² – 1 .

Производные высших порядков

( ln x )⁽ⁿ⁾ = (–1)^n – 1 (n – 1)!xⁿ.
См. Доказательство методом математической индукции >>>

( x^m )⁽ⁿ⁾ = m (m – 1) ...   (m – n + 1) x^m – n.
См. Вывод производной степенной функции n-го порядка >>>

( a^x )⁽ⁿ⁾ = a^x  lnⁿ a.
См. Производные высших порядков показательной функции >>>

Тригонометрические функции

( sin x )⁽ⁿ⁾ = sin( x + nπ2 ).
См. Доказательство методом математической индукции >>>

( cos x )⁽ⁿ⁾ = cos( x + nπ2 ).
См. Производные косинуса высших порядков >>>

(tg x)⁽ⁿ⁾ = [ ( 1 + y² ) ddy  ]ⁿ y,
где y = tg x.
См. Производные тангенса высших порядков >>>.

(ctg x)⁽ⁿ⁾ = (–1)ⁿ [ ( 1 + y² ) ddy  ]ⁿ y,
где y = ctg x.
См. Производные котангенса высших порядков >>>.

Обратные тригонометрические функции

Производные арксинуса и арккосинуса

(arcsin x)⁽ⁿ⁾ = p_n (x)( 1 – x² )^n – 12,
где p_n (x) – многочлен степени n – 1. Он определяется по формулам:
p_2m + 1 (x) = A [1 + ^mΣ_k = 1 (m!)²(2k)!( (m – k)! )² (2x)^2k];
p_2m (x) = Ax [1 + ^m – 1Σ_k = 1 ((m – 1)!)²(2k + 1)!( (m – k – 1)! )² (2x)^2k].
Здесь A = [1 ⋅ 3 ⋅ 5⋅ ⋅ ⋅(2m – 1)]² ≡ [(2m – 1)!!]².
(arccos x )⁽ⁿ⁾ = –(arcsin x )⁽ⁿ⁾.
См. Вывод производных высших порядков арксинуса и арккосинуса >>>.

Производные арктангенса и арккотангенса

(arctg x)⁽ⁿ⁾ = (–1)^n + 1  (n – 1)! ⋅ Im (x + i)ⁿ(1 + x²)ⁿ;
(arcctg x)⁽ⁿ⁾ = –(arctg x)⁽ⁿ⁾ = (–1)ⁿ  (n – 1)! ⋅ Im (x + i)ⁿ(1 + x²)ⁿ.

Другой вид производных:
y⁽ⁿ⁾ = (n – 1)!  cosⁿ y ⋅ sin[ n( y + π2 ) ],
где y = arctg x.
z⁽ⁿ⁾ = (n – 1)!  sinⁿ z ⋅ sin[n( z + π )],
где z = arcctg x.

См. Вывод производных высших порядков арктангенса и арккотангенса >>>.