Вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x)

Представлен вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x). Производные даны в двух видах - выраженные через независимую переменную x и через арктангенс (арккотангенс). Вычислены производные от второго до пятого порядка.

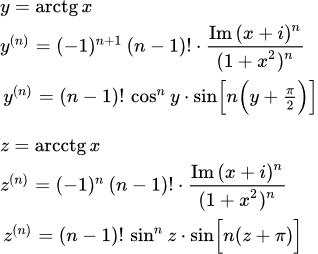
Вывод производных высших порядков арктангенса

Пусть y = arctg x. Считаем, что нам известна производная арктангенса первого порядка:
(1)   y^′ = 11 + x².

Найдем производные высших порядков. Для этого разложим дробь на простейшие:
11 + x² = 1(x – i)(x + i) = 12i x + i – (x – i)(x – i)(x + i) = 12i (  1x – i – 1x + i ) =
 i2 (  1x + i – 1x – i ).
Здесь i – мнимая единица, i² = –1.

Тогда производную арктангенса первого порядка можно записать в следующем виде:
y^′ = i2 (  1x + i – 1x – i ).

Дифференцируем n – 1 раз и приводим дроби к общему знаменателю:
y⁽ⁿ⁾ = (–1)^n – 1 (n – 1)! i2 (  1(x + i)ⁿ –   1(x – i)ⁿ ) =
 (–1)^n – 1 i (n – 1)! ⋅ (x – i)ⁿ – (x + i)ⁿ2(1 + x²)ⁿ = (–1)ⁿ i (n – 1)! ⋅ (x + i)ⁿ – (x – i)ⁿ2(1 + x²)ⁿ.
В числителе стоит разность комплексно сопряженных величин. Поэтому числитель является чисто мнимым. Пусть  Im  обозначает мнимую часть стоящего следом выражения. Тогда производную арктангенса n-го порядка можно записать в следующем виде:
(2)   y⁽ⁿ⁾ = (–1)^n + 1  (n – 1)! ⋅ Im (x + i)ⁿ(1 + x²)ⁿ.
Здесь выражение в числителе является многочленом степени n – 1.

Производные арктангенса со второго по пятый порядок

Вычислим производные арктангенса нескольких высших порядков, используя формулу (2). Для этого мы используем формулу бинома Ньютона:
(a + b)ⁿ = aⁿ + na^n – 1 b + n(n – 1)2! a^n – 2 b²+...  + n!(n – k)! k! a^n – k b^k+... +bⁿ.
Также используем свойства мнимой единицы:
i² = –1;
i³ = i² ⋅ i = –i;
i⁴ = i² ⋅ i² = (–1) ⋅ (–1) = 1.
И так далее.

Производная второго порядка.
При n = 2 имеем:
(x + i)² = x² + 2xi + i² = x² + 2xi – 1;
Im (x + i)² = 2x;
y^′′ = y⁽²⁾ = (–1)^2 + 1  (2 – 1)! ⋅ Im (x + i)²(1 + x²)² = – 2x(1 + x²)².

Производная третьего порядка.
При n = 3 имеем:
(x + i)³ = x³ + 3x² i + 3xi² + i³ = x³ + 3x² i – 3x – i;
Im (x + i)³ = 3x² – 1;
y^′′′ = y⁽³⁾ = (–1)^3 + 1  (3 – 1)! ⋅ Im (x + i)³(1 + x²)³ = –2 ⋅ 1 – 3x²(1 + x²)³.

Производная четвертого порядка.
При n = 4 получаем:
(x + i)⁴ = x⁴ + 4x³ i + 6x² i² + 4xi³ + i⁴ = x⁴ + 4x³ i – 6x² – 4xi + 1;
Im (x + i)⁴ = 4x³ – 4x;
y^IV = y⁽⁴⁾ = (–1)^4 + 1  (4 – 1)! ⋅ Im (x + i)⁴(1 + x²)⁴ = –6 ⋅ 4x³ – 4x(1 + x²)⁴ = 24 ⋅ x – x³(1 + x²)⁴.

Наконец, вычислим производную пятого порядка.
Подставим n = 5:
(x + i)⁵ = x⁵ + 5x⁴ i + 10x³ i² + 10x² i³ + 5xi⁴ + i⁵ =
 x⁵ + 5x⁴ i – 10x³ – 10x² i + 5x + i;
Im (x + i)⁵ = 5x⁴ – 10x² + 1;
y^V = y⁽⁵⁾ = (–1)^5 + 1  (5 – 1)! ⋅ Im (x + i)⁵(1 + x²)⁵ = 24 ⋅ 1 – 10x² + 5x⁴(1 + x²)⁵.

Другой вид производных арктангенса высших порядков

Оказывается, что формулу производной арктангенса n-го порядка можно представить в удобном виде, если выразить производную не через независимую переменную x, а через сам арктангенс.

Итак, пусть
y = arctg x.
Используем формулу (2) производной n-го порядка:
(2)   y⁽ⁿ⁾ = (–1)^n + 1  (n – 1)! ⋅ Im (x + i)ⁿ(1 + x²)ⁿ.
Подставим x = tg y:
1 + x² = 1 + tg² y = cos² y + sin² ycos² y = 1cos² y;
1(1 + x²)ⁿ = cos²ⁿ y;
x + i = tg y + i = sin y + i cos ycos y = i cos y – i sin ycos y = i e^–iycos y = –e^{–iπ / 2} e^–iycos y =
 – e^{–i( y + π2 )}cos y;
(x + i)ⁿ = (–1)ⁿ e^{–in( y + π2 )}cosⁿ y.
Применим формулу Эйлера. Тогда
e^{–in( y + π2 )} = cos[ n( y + π2 ) ] – i sin[ n( y + π2 ) ];
Im  e^{–in( y + π2 )}= –sin[ n( y + π2 ) ];
Im (x + i)ⁿ = (–1)^n + 1 sin[ n( y + π2 ) ]cosⁿ y;
y⁽ⁿ⁾ = (–1)^n + 1  (n – 1)! ⋅ 1(1 + x²)ⁿ ⋅ Im (x + i)ⁿ =
 (–1)^n + 1  (n – 1)! ⋅ cos²ⁿ y ⋅ (–1)^n + 1 sin[ n( y + π2 ) ]cosⁿ y = (n – 1)!  cosⁿ y ⋅ sin[ n( y + π2 ) ].

Тем самым мы получили производную арктангенса n-го порядка, выраженную через сам арктангенс:
(3)   y⁽ⁿ⁾ = (n – 1)!  cosⁿ y ⋅ sin[ n( y + π2 ) ].
Здесь   y = arctg x.

Производные высших порядков арккотангенса

Чтобы получить производные высших порядков арккотангенса, воспользуемся связью между арктангенсом и арккотангенсом:
(4)   arcctg x = π2 – arctg x.
Дифференцируя это уравнение n раз и учитывая, что производная постоянной π / 2 равна нулю, получим производную арккотангенса n-го порядка:
(5)   (arcctg x)⁽ⁿ⁾ = –(arctg x)⁽ⁿ⁾ = (–1)ⁿ  (n – 1)! ⋅ Im (x + i)ⁿ(1 + x²)ⁿ.

Другой вид производных арккотангенса высших порядков

Пусть
z = arcctg x.
Выразим производную n-го порядка арккотангенса через z. Для этого можно подставить в (5) x = ctg z. Но мы используем формулу (3) для n-ой производной арктангенса и формулу (4), связывающую арккотангенс с арктангенсом. Пусть
y = arctg x.
Тогда y = π / 2 – z. Подставим в (3):
(3)   y⁽ⁿ⁾ = (n – 1)!  cosⁿ y ⋅ sin[ n( y + π2 ) ];
–z⁽ⁿ⁾ = (n – 1)!  cosⁿ (  π2 – z ) ⋅ sin[ n(  π2 – z + π2 ) ].
Далее замечаем, что
cos(  π2 – z ) = sin z;
sin[n( π – z )] = –sin[n( z – π )] = –sin[n( z + π )].
Тогда
(6)   z⁽ⁿ⁾ = (n – 1)!  sinⁿ z ⋅ sin[n( z + π )].
Это и есть искомая формула производной n-го порядка арккотангенса.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 17-05-2017