Примеры применения формулы производной сложной функции

Приводятся примеры вычисления производных сложных функций.

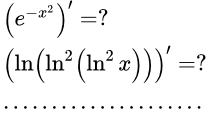
Формула производной сложной функции

Если функцию можно представить как сложную:
,
то ее производная определяется по формуле производной сложной функции:
.
Ее можно записать в нескольких вариантах, например:
.
Или так:
.
где .
Здесь нижние индексы или , под знаком производной, обозначают переменные, по которой выполняется дифференцирование. Для функций в этом нет необходимости, поскольку по умолчанию дифференцирование выполняется по аргументу. Для переменной y нижний индекс необходим, поскольку ее можно выразить как через x, так и через u:
.

Обычно, в таблицах производных аргумент функции обозначают буквой x. Однако x – это формальный параметр. Обозначение x можно заменить любой буквой или символом. Поэтому, при дифференцировании функции, зависящей от переменной , мы просто меняем, в таблице производных, x на u.

Примеры

Далее рассмотрены примеры решений производной сложной функции.
Простые примеры.
   
Более сложные примеры
 

Простые примеры

Пример 1

Найти производную сложной функции
.

Решение

Запишем заданную функцию в эквивалентном виде:
.
В таблице производных находим:
;
.

По формуле производной сложной функции имеем:
.
Здесь .

Ответ

.

Пример 2

Найти производную
.

Решение

Выносим постоянную 5 за знак производной и из таблицы производных находим:
.

Применяем формулу производной сложной функции:
.
Здесь .

Ответ

.

Пример 3

Найдите производную
.

Решение

Выносим постоянную –1 за знак производной и из таблицы производных находим:
;
Из таблицы производных находим:
.

Применяем формулу производной сложной функции:
.
Здесь .

Ответ

.

Более сложные примеры

В более сложных примерах мы применяем правило дифференцирования сложной функции несколько раз. При этом мы вычисляем производную с конца. То есть разбиваем функцию на составные части и находим производные самых простых частей, используя таблицу производных. Также мы применяем правила дифференцирования суммы, произведения и дроби. Затем делаем подстановки и применяем формулу производной сложной функции.

Пример 4

Найдите производную
.

Решение

Выделим самую простую часть формулы и найдем ее производную. .

Применяем правило дифференцирования сложной функции.

.
Здесь мы использовали обозначение
.

Находим производную следующей части исходной функции, применяя полученные результаты. Применяем правило дифференцирования суммы:
.

Еще раз применяем правило дифференцирования сложной функции.

.
Здесь .

Ответ

.

Пример 5

Найдите производную функции
.

Решение

Выделим самую простую часть формулы и из таблицы производных найдем ее производную. .

Применяем правило дифференцирования сложной функции.
.
Здесь
.

Дифференцируем следующую часть, применяя полученные результаты.
.
Здесь
.

Дифференцируем следующую часть.

.
Здесь
.

Теперь находим производную искомой функции.

.
Здесь
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 19-11-2016