Теорема о производной обратной функции
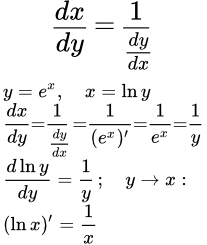
Теорема
Пусть функция
(1) y = f (x)
непрерывна и строго монотонна в некоторой окрестности точки x0. И пусть в этой точке x = x0 существует отличная от нуля производная f ′(x0) ≠ 0. Тогда обратная функция
(2) x = f –1 (y)
имеет в точке y0 = f (x0) производную, равную обратной величине производной исходной функции:
(3) ( f –1) ′(y0) = 1 f ′(x0).
Разумеется, можно использовать любые обозначения для переменных. Так, вместо (3) можно написать так:
( f –1) ′(y) = 1 f ′(x).
При этом функция f (x) должна быть непрерывной и строго монотонной в окрестности точки x. Формулу (3) можно записать через дифференциалы. Тогда она примет наиболее простой вид:
(4) dxdy = 1dydx.
Доказательство
1. Поскольку функция y = f (x) непрерывна и строго монотонна в некоторой окрестности U(x0) точки x0, то согласно теореме о существовании и непрерывности обратной функции на интервале, существует такая окрестность точки y0 = f (x0), на которой определена обратная функция x = f –1 (y), которая непрерывна и строго монотонна на этой окрестности.
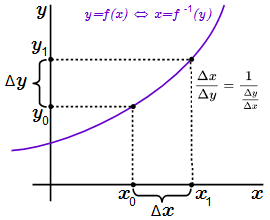
2. Возьмем точку x1, расположенную в рассматриваемой окрестности U(x0). Ее образ обозначим как y1 = f (x1). Вводим новые переменные Δx и Δy, называемые приращениями переменных: Δx = x1 – x0; Δy = y1 – y0. Выпишем все используемые обозначения, связанные с отображением точек (x0, y0) и(x1, y1) функцией f и обратной к ней функции f–1:
(5) y0 = f (x0); y1 = f (x1); Δx = x1 – x0;
(6) x0 = f –1 (y0); x1 = f –1 (y1); Δy = y1 – y0.
Используем очевидное алгебраическое соотношение:
(7) ΔxΔy = 1ΔyΔx; Δx ≠ 0, Δy ≠ 0.
Как отмечено, оно выполняется при Δx ≠ 0 и Δy ≠ 0. Преобразуем отношение приращения обратной функции к приращению ее аргумента, используя (7) и обозначения (5) и (6):
f –1 (y0 + Δy) – f –1 (y0)Δy = f –1 (y1) – f –1 (y0)y1 – y0 = x1 – x0y1 – y0 = ΔxΔy = ( ΔyΔx ) –1 =
( y1 – y0x1 – x0 ) –1 = ( f (x1) – f (x0)x1 – x0 ) –1 = ( f (x0 + Δx) – f (x0)Δx ) –1.
Итак, мы получили следующее алгебраическое соотношение:
(8) f –1 (y0 + Δy) – f –1 (y0)Δy = 1 f (x0 + Δx) – f (x0)Δx.
3. Теперь выполним предельный переход Δy → 0. Для этого мы намерены применить теорему о пределе сложной функции. Поэтому представим выражение в левой части (8) как сложную функцию.
Считаем, что x0 и y0 являются фиксированными числами. Нам нужно найти предел при Δy → 0 от следующей функции, зависящей от переменной Δy:
(9) p(Δy) = f –1 (y0 + Δy) – f –1 (y0)Δy.
Мы обозначили ее как p(Δy). Тогда уравнение (8) можно рассматривать как эту же функцию, выраженную через переменную Δx. Обозначим ее как q(Δx):
(10) q(Δx) = 1 f (x0 + Δx) – f (x0)Δx.
Сюда нужно еще добавить отображение, связывающее переменные Δx и Δy. Такое отображение мы обозначим как Δx(Δy):
(11) Δx(Δy) = f –1 (y0 + Δy) – f –1 (y0).
Тогда функцию p можно рассматривать как сложную:
(12) p(Δy) = q(Δx(Δy)).
Можно непосредственно убедиться в справедливости (12). Для этого подставим (11) в (10):
q(Δx(Δy)) = ( f (x0 + Δx(Δy)) – f (x0)Δx(Δy) ) –1.
Выполняем преобразования, используя (5), (6) и (11):
f (x0 + Δx(Δy)) – f (x0) = f ( f –1 (y0) + f –1 (y0 + Δy) – f –1 (y0)) – y0 =
f ( f –1 (y0 + Δy)) – y0 = y0 + Δy – y0 = Δy;
Δx(Δy) = f –1 (y0 + Δy) – f –1 (y0);
q(Δx(Δy)) = ( f (x0 + Δx(Δy)) – f (x0)Δx(Δy) ) –1 = f –1 (y0 + Δy) – f –1 (y0)Δy = p(Δy).
Все верно.
4. Теперь применяем теорему о пределе сложной функции. к пределу
limΔy → 0 p(Δy) = limΔy → 0 q(Δx(Δy)),
где
(9) p(Δy) = f –1 (y0 + Δy) – f –1 (y0)Δy;
(10) q(Δx) = 1 f (x0 + Δx) – f (x0)Δx;
(11) Δx(Δy) = f –1 (y0 + Δy) – f –1 (y0).
1) Как было указано в самом начале доказательства, обратная функция f –1 определена и непрерывна в некоторой окрестности точки y0. Тогда согласно определению непрерывности функции в точке в терминах приращений,
(13) limΔy → 0 Δx(Δy) = 0.
2) Теперь нам нужно показать, что существует такая проколотая окрестность точки Δy = 0, в которой Δx(Δy) ≠ 0.
Рассмотрим точку Δy = 0. Из (6) следует, что при этом Δx = x1 – x0 = 0. Действительно, тогда y1 = y0; x1 = f –1 (y1) = f –1 (y0) = x0; Δx = x1 – x0 = 0. Поскольку, как было указано в самом начале доказательства, обратная функция f –1 строго монотонна, то она принимает значение x0 только в одной точке y0. Следовательно, переменная Δx принимает нулевое значение Δx = 0 только в одной точке, в которой Δy = 0. Поэтому
(14) если Δy ≠ 0, то и Δx ≠ 0.
3) Находим предел от q(Δx) = 1 f (x0 + Δx) – f (x0)Δx при Δx → 0. Предел в знаменателе равен производной функции f в точке x0, которая существует по условию теоремы:
limΔx → 0 f (x0 + Δx) – f (x0)Δx = f ′(x0).
По условию, f ′(x0) ≠ 0. Применяем арифметические свойства предела функции:
limΔx → 0 q(Δx) = limΔx → 0 1 f (x0 + Δx) – f (x0)Δx = 1limΔx → 0 f (x0 + Δx) – f (x0)Δx = 1 f ′(x0).
Все предварительные вычисления и условия теоремы о пределе сложной функции выполнены. Находим производную обратной функции:
( f –1) ′(y0) = limΔy → 0 f –1 (y0 + Δy) – f –1 (y0)Δy = limΔy → 0 p(Δy) = limΔy → 0 q(Δx(Δy)) =
limΔx → 0 q(Δx) = 1 f ′(x0).
Теорема доказана.
Примеры
Производная натурального логарифма
Рассмотрим экспоненту (экспоненциальную функцию), y = e x. Она определена и строго возрастает для всех значений аргумента x. Экспонента имеет производную, равную самой функции: y ′ = e x.
Обратной к экспоненте является натуральный логарифм, x = ln y. Он определен и строго возрастает при положительных значениях аргумента y > 0. Найдем его производную, применяя теорему о производной обратной функции.
(ln y) ′y = d ln ydy = dxdy = 1dydx = 1(e x) ′x = 1e x = 1y.
Итак, мы нашли производную натурального логарифма, выраженную через переменную y:
(ln y) ′y = 1y.
Переменные мы можем обозначать любыми буквами. Поэтому, поменяем y на x:
(ln x) ′ = 1x.
Производная арксинуса
Рассмотрим функцию синус, y = sin x. Синус строго возрастает при – π2 ≤ x ≤ π2. Поэтому на этом интервале определена обратная функция, которая называется арксинусом, x = arcsin y, –1 ≤ y ≤ 1. См. «Доказательство непрерывности тригонометрических функций»
Находим производную арксинуса, применяя теорему о производной обратной функции.
(arcsin y) ′y = dxdy = 1dydx = 1(sin x) ′ = 1cos x.
Итак, мы получили:
(arcsin y) ′y = 1cos x.
Теперь нужно выразить правую часть через переменную y = sin x. Поскольку при – π2 ≤ x ≤ π2, cos x ≥ 0, то cos x = + √ 1 – sin 2 x = √ 1 – y 2 . Тогда
(arcsin y) ′y = 1cos x = 1√ 1 – y 2 .
Наконец, заменив переменную y на букву x, получаем формулу производной арксинуса, записанную в привычном виде:
(arcsin x) ′ = 1√ 1 – x 2 .
Автор: Олег Одинцов. Опубликовано: