Формула Лейбница для n-й производной произведения двух функций
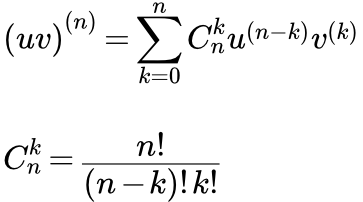
Формула Лейбница
С помощью формулы Лейбница можно вычислить производную n-го порядка от произведения двух функций. Она имеет следующий вид:
(1) ,
где
– биномиальные коэффициенты.
Биномиальные коэффициенты являются коэффициентами разложения бинома по степеням и :
.
Также число является числом сочетаний из n по k.
Доказательство формулы Лейбница
Доказательство первым способом
Применим формулу производной произведения двух функций:
(2) .
Перепишем формулу (2) в следующем виде:
.
То есть мы считаем, что одна функция зависит от переменной x, а другая – от переменной y. В конце расчета мы полагаем . Тогда предыдущую формулу можно записать так:
(3) .
Поскольку производная равна сумме членов, и каждый член является произведением двух функций, то для вычисления производных высших порядков, можно последовательно применять правило (3).
Тогда для производной n-го порядка имеем:
.
Учитывая, что и , мы получаем формулу Лейбница:
(1) .
Доказательство методом индукции
Приведем доказательство формулы Лейбница методом математической индукции.
Еще раз выпишем формулу Лейбница:
(4) .
При n = 1 имеем:
.
Это формула производной произведения двух функций. Она справедлива.
Предположим, что формула (4) справедлива для производной n-го порядка. Докажем, что она справедлива для производной n + 1-го порядка.
Дифференцируем (4):
;
.
Итак, мы нашли:
(5) .
Далее замечаем, что
;
;
.
Подставим в (5) и учтем, что :
.
Отсюда видно, что формула (4) имеет тот же вид и для производной n + 1-го порядка.
Итак, формула (4) справедлива при n = 1. Из предположения, что она выполняется, для некоторого числа n = m следует, что она выполняется для n = m + 1.
Формула Лейбница доказана.
Пример
Все примеры Вычислить n-ю производную функции
.
Решение
Применим формулу Лейбница
(2) .
В нашем случае
;
.
Находим производные от функции .
По таблице производных имеем:
.
Применяем свойства тригонометрических функций:
.
Тогда
.
Отсюда видно, что дифференцирование функции синус приводит к ее сдвигу на . Тогда
.
Находим производные от функции .
;
;
;
, .
Поскольку при , то в формуле Лейбница отличны от нуля только первые три члена. Находим биномиальные коэффициенты.
;
.
По формуле Лейбница имеем:
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
