Производная тангенса: (tg x)′

Представлен вывод формулы для производной тангенса - tg(x). Примеры вычисления производных от tg 2x, tg 3x и tg nx. Производная тангенса n-го порядка в виде многочлена по степеням tg(x).

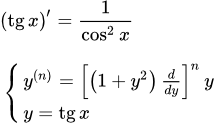
Производная по переменной x от тангенса x равна единице, деленной на косинус в квадрате от x:
(tg x)^′ = 1cos² x.

Вывод формулы производной тангенса

Производные синуса и косинуса определены для всех значений переменной x. Формула производной дроби (4) справедлива для тех значений переменной x, в которых существуют производные функций u и v и для которых знаменатель дроби не обращается в нуль:
v ≠ 0.
Таким образом, производная тангенса справедлива для всех x, кроме точек, в которых cos x = 0. То есть кроме точек
x = π2 + nπ,
где n = 0, ±1, ±2, ±3, ... – целое число.
С другой стороны, сама функция y = tg x определена для всех x, кроме точек
x = π2 + nπ.
Поэтому производная тангенса определена на всей области определения тангенса.

Пример

Найти производные от tg 2x, tg 3x и tg nx.

Решение

Найдем производную от функции tg nx.
Представим эту функцию как сложную, состоящую из двух функций:
1)   Функции u = nx, зависящей от переменной x:  u = u(x);
2)   Функции  f  = tg u, зависящей от переменной u:   f  =  f (u).
Тогда исходная функция y(x) является сложной функцией, составленной из функций  f  и u:
y(x) =  f  (u(x)).

Найдем производную от функции u по переменной x:
u^′ = (nx)^′ = n(x)^′ = n(x¹)^′ = n ⋅ 1 ⋅ x^1 – 1 = nx⁰ = n ⋅ 1 = n.
Найдем производную от функции  f  по переменной u:
 f ^′_u = (tg u)^′_u = 1cos² u.
Применяем правило дифференцирования сложной функции:
y^′_x =  f ^′_u ⋅ u^′_x = 1cos u ⋅ n = ncos² u.
Заменим u = nx:
y^′ = ( tg nx )^′ = ncos² nx.

Подставляя вместо n значения n = 2 и n = 3, получаем производные функций tg 2x и tg 3x:
( tg 2x )^′ = 2cos² 2x;
( tg 3x )^′ = 3cos² 3x.

Ответ

( tg 2x )^′ = 2cos² 2x;
( tg 3x )^′ = 3cos² 3x;
( tg nx )^′ = ncos² nx.

См. также
Все примеры вычисления производных с решениями > > >

Производные высших порядков

К сожалению, простой формулы, для производной n-го порядка от функции y = tg x, нет. Однако, если требуется найти производные высшего порядка, то процесс дифференцирования можно упростить и свести его к дифференцированию многочлена.

Для этого заметим, что производную от тангенса можно выразить через сам тангенс (через саму функцию):
y^′ = ( tg x )^′ = 1cos² x = cos² x + sin² xcos² x = 1 + tg² x = 1 + y².
Тем самым мы нашли дифференциальное уравнение, которому удовлетворяет тангенс:
(6)   y^′ = 1 + y².

Найдем производную второго порядка, дифференцируя уравнение (6) и применяя правило дифференцирования сложной функции:
y^′′ = ( y^′ )^′ = ( 1 + y² )^′_y ⋅ y^′ = 2y ⋅ y^′.
Подставим (6):
(7)   y^′′ = 2y( 1 + y² ) = 2( y + y³ ).

Найдем производную третьего порядка. Для этого дифференцируем уравнение (7) и применяем правило дифференцирования сложной функции. Также используем выражение (6) для первой производной:
y^′′′ = 2( y + y³ )^′_y ⋅ y^′ = 2( 1 + 3y² ) ⋅ ( 1 + y² ) = 2( 1 + 4y² + 3y⁴ ).

Аналогичным способом находим производные четвертого и пятого порядков:
y^IV = 2( 1 + 4y² + 3y⁴ )^′_y ⋅ y^′ = 2( 8y + 12y³ ) ⋅ ( 1 + y² ) = 8( 2y + 3y³ ) ⋅ ( 1 + y² ) =
 8( 2y + 5y³ + 3y⁵ );
y^V = 8( 2y + 5y³ + 3y⁵ )^′_y ⋅ y^′ = 8( 2 + 15y² + 15y⁴ ) ⋅ ( 1 + y² ) =
 8( 2 + 17y² + 30y⁴ + 15y⁶ ).

В общем виде, производную n-го порядка, по переменной x от функции тангенс, y = tg x, можно представить в виде многочлена по степеням тангенса:
y⁽ⁿ⁾ = ^n + 1Σ_k = 0 aⁿ_k y^k.
Коэффициенты aⁿ_k связаны рекуррентным соотношением:
a^n + 1_k = (k – 1) aⁿ_k – 1 + (k + 1) aⁿ_k + 1,
где
a⁰₀ = 0;   a⁰₁ = 1;
a^m_–1 = 0;  a^m_m + 2 = 0;  a^m_m + 3 = 0;   m = 1,  2,  3, ....

Общая формула

Процесс дифференцирования можно представить одной формулой. Для этого заметим, что
y^(n + 1) = ( y⁽ⁿ⁾ )^′ = ( y⁽ⁿ⁾ )^′_y ⋅ y^′ = y^′ ⋅ ddy y⁽ⁿ⁾ = ( 1 + y² ) ⋅ ddy y⁽ⁿ⁾.
Тогда n-я производная тангенса имеет следующий вид:
y⁽ⁿ⁾ = [ ( 1 + y² ) ddy  ]ⁿ y,
где y = tg x.

Автор: Олег Одинцов.     Опубликовано: 09-03-2017