Свойства показательной функции

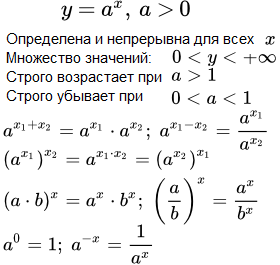
Теорема. Свойства показательной функции

Показательная функция
имеет на множестве действительных чисел x следующие свойства:
(0)   определена, при , для всех ;  ⇓
(1)   при a ≠ 1 имеет множество значений ;  ⇓
(2)   строго возрастает при , строго убывает при , является постоянной при ;  ⇓
(3)   ;  ⇓
(3*)   ;  ⇓
(4)   ;  ⇓
(5)   ;  ⇓
(5*)   ;  ⇓
(6)   ;  ⇓
(7)   ;  ⇓
(8)   непрерывна для всех ;  ⇓
(9)     при ;
  при .  ⇓

Доказательство теоремы

При доказательстве мы считаем, что свойства показательной функции на множестве рациональных чисел известны. Их вывод изложен на странице «Определение и свойства показательной функции».

Поэтому нам нужно доказать свойства функции , определенной на множестве действительных чисел: . Для этого мы используем определение показательной функции, как предела последовательности:
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x:
.

Заметим, что для доказательства свойств показательной функции, нам достаточно выбрать любую, удобную для нас последовательность рациональных чисел , сходящуюся к x. Действительно, согласно лемме, значение не зависит от выбора последовательности.

Порядок доказательств свойств показательной функции отличается от порядка, в котором расположены свойства. Это сделано для удобства изложения. Последующие пункты могут использовать свойства, доказанные в первую очередь.

a^x > 0

А. Сначала докажем, что
(С.А.1)   a^x > 0.
Согласно определению,
.
Поскольку последовательность рациональных чисел сходится к конечному числу x, то она ограничена:
.
Поскольку функция , определенная на множестве рациональных чисел монотонна (см. (1.2)), то она достигает своего минимального значения на границе рассматриваемого отрезка. Тогда
(С.А.2)   .
Здесь при нужно взять знак “плюс”. При – знак “минус”. При , функция постоянна, . Можно взять любой знак. Выполним в (С.А.2) предельный переход , пользуясь свойствами пределов последовательностей, связанными неравенствами и определением показательной функции:
;
.
Согласно свойству (1.1), . Тогда и
.

Область определения

0. ⇑ Докажем, что показательная функция
определена, при , для всех действительных чисел .
Поскольку показательная функция , при , определена для всех рациональных чисел r, и поскольку для любого действительного числа x существует последовательность рациональных чисел, сходящихся к x, то, согласно определению, показательная функция определена для всех действительных чисел .

6. a⁰ = 1

6. ⇑ .
Здесь аргумент является рациональным числом. Мы считаем, что свойства показательной функции на множестве рациональных чисел известны. Мы добавили этот пункт, чтобы объединить все свойства вместе.

2. Строгая монотонность

2. ⇑ Докажем строгую монотонность показательной функции при a ≠ 1. То есть, если , то
при ;
при ;
при .

Итак, пусть . Выберем рациональные числа и , удовлетворяющие неравенствам:
.
Возьмем последовательности и , сходящиеся к и :
,
элементы которых удовлетворяют неравенствам:
,   .
Тогда
.

2.1. Пусть .
Поскольку показательная функция, определенная на множестве рациональных чисел, при , строго возрастает, то
(С.2.1)   .
Применим свойства пределов последовательностей, связанных неравенствами и определение показательной функции:
;
.
Отсюда .

2.2. Пусть .
В этом случае, показательная функция, определенная на множестве рациональных чисел, строго убывает. Доказательство такое же, как и в пункте 2.1 ⇑, только начиная с (С.2.1), нужно поменять знаки неравенств:
(С.2.2)   ;
;
;
.

2.3. Пусть .
Показательная функция , определенная на множестве рациональных чисел , является постоянной . Последовательность является последовательностью из постоянных элементов. Поэтому ее предел также равен единице:
;
  для всех x.

3. a^x₁+x₂ = a^x₁ · a^x₂

3. ⇑ Докажем, что
.
Пусть и – произвольные последовательности рациональных чисел, сходящиеся к и :
.
Применим свойство предела суммы для последовательности :
(С.3.1)   .
Рассмотрим последовательность . Поскольку, согласно лемме, и сходятся, то применим свойство предела произведения последовательностей иопределение показательной функции:
.
С другой стороны, применяя (С.3.1) и свойство (1.3) показательной функции от рационального аргумента, имеем:
.
Отсюда
.

5. (a·b)^x = a^x · b^x

5. ⇑ Докажем, что
.
Все рассуждения и обозначения такие же, что и при доказательстве свойства 3 ⇑. Аналогичным образом, применяя свойство (1.5) для рационального аргумента, имеем:
.

5*. (a/b)^x = a^x / b^x

5*. ⇑ Докажем, что
.
Используем следующее свойство показательной функции от рационального аргумента: . Доказываем тем же способом, что и в предыдущем случае.
.

7. a^–x = 1 / a^x

7. ⇑ Докажем, что
.
Аналогично предыдущему, имеем:
.
Здесь мы учли, что и применили свойство предела частного последовательностей.

3*. a^x₁–x₂ = a^x₁ / a^x₂

3*. ⇑ Докажем, что
.
Применяя доказанные выше свойства 3 ⇑ и 7 ⇑, имеем:
.

8. Непрерывность

8. ⇑ Докажем, что показательная функция
непрерывна для всех .

8.1. Пусть .
Воспользуемся определением непрерывности функции в терминах приращений. Применяем свойство a^x > 0 ⇑ и 3 ⇑
.
Поскольку есть сколь угодно малая величина, то считаем, что . Применим лемму Бернулли для действительных чисел:
.
Тогда
.
Применяем свойство пределов функций, связанных неравенством:
;
;
.

8.2. Пусть .
Введем число . Тогда .
Воспользуемся свойством 5* ⇑, и учтем, что – постоянная функция:
.
Рассмотрим функцию как сложную, составленную из двух функций:
. Выше мы доказали, что функция непрерывна для всех x. Функция непрерывна при . Это можно доказать, применяя арифметические свойства предела функции:
.
Выше мы доказали ⇑, что . Тогда согласно теореме о непрерывности сложной функции, функция непрерывна для всех x.

8.3. Пусть .
Выше мы показали ⇑, что функция является постоянной функцией: . Поэтому она является непрерывной для всех x.

4. a^x₁·x₂ = (a^x₁)^x₂

4. ⇑ Докажем, что
.

4.1. Рассмотрим случай .
Пусть – натуральные числа. Тогда
.
Применяя свойство 3 ⇑, имеем:
;
(С.4.1)   .

Теперь исследуем, что такое . Введем обозначение:
(С.4.2)   .
Возведем в n-ю степень. То есть умножим левую и правую части на себя n раз, и применим (С.4.1):
;
.
Поскольку a^x > 0 ⇑, то b есть корень степени n из положительного числа :
. Подставляя (С.4.2), имеем:
(С.4.3)   .

Применяя свойства (С.4.1) и (С.4.3), для произвольного положительного рационального числа получаем:
;
(С.4.4)   .

Пусть есть произвольная последовательность рациональных чисел, сходящаяся к x₂:
(С.4.5)   .
Используем (С.4.4):
.
Рассмотрим последовательность . Учитывая (С.4.5), и применяя арифметические свойства сходящихся последовательностей, получаем, что сходится к :
.
Выше мы доказали, что показательная функция непрерывна ⇑. Используя определение непрерывности функции по Гейне, получаем:
;
.
Что и требовалось доказать.

4.2. Рассмотрим случай .
Тогда . Применяя свойство 7 ⇑, имеем:
.

4.3. Теперь пусть .
Применяем (С.6) Тогда .
Поскольку a^x₁ > 0 ⇑, то
.
Таким образом и в этом случае
.

9. Пределы при x → ±∞

9. ⇑ Докажем, что
  при ;
  при .
9.1. Пусть .
9.1.1. Докажем, что
.
Поскольку функция монотонна ⇑, то согласно теореме о пределе монотонной функции, она имеет конечный или бесконечный предел
.
Поскольку функция имеет предел A, то согласно определению предела функции по Гейне, для любой последовательности , сходящейся к , последовательность сходится к A:
.
Возьмем последовательность натуральных чисел . Она сходится к : . Тогда
.

Для вычисления этого предела, применим неравенство Бернулли:
.
При , правая часть неравенства стремится к . Применяя свойство неравенств бесконечно больших последовательностей, находим, что
.
Отсюда ,  .

9.1.2. Докажем, что
.
Сделаем подстановку . Применим свойство (С.7)   и свойства бесконечно малых и бесконечно больших функций:
.

9.2. Пусть .
Сделаем подстановку . Тогда ,
;
.

1. Множество значений

1. ⇑ Докажем, что при a ≠ 1 показательная функция имеет множество значений .
Рассмотрим функцию на отрезке , где – произвольные числа. Поскольку функция строго монотонна ⇑ и определена для всех x, то она достигает минимума и максимума на концах отрезка – в точках и . Поскольку функция непрерывна ⇑, то согласно теореме Больцано – Коши о промежуточном значении, она принимает все значения из отрезка , если и , если . Устремляя и , и используя найденные выше пределы ⇑ получаем, что множеством значений показательной функции является множество положительных чисел .

Теорема доказана.