Производная синуса: (sin x)′
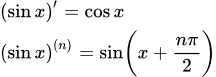
Производная по переменной x от синуса x равна косинусу x:
( sin x )′ = cos x.
Доказательство
Для вывода формулы производной синуса, мы воспользуемся определением производной:
( sin x ) ′ = limΔx → 0 sin(x + Δx) – sin xΔx.
Чтобы найти этот предел, нам нужно преобразовать выражение таким образом, чтобы свести его к известным законам, свойствам и правилам. Для этого нам нужно знать четыре свойства.
1) Значение первого замечательного предела:
(1) limt → 0 sin tt = 1;
2) Непрерывность функции косинус:
(2) limt → 0 cos(x + t) = cos(x);
3) Тригонометрические формулы. Нам понадобится следующая формула:
(3) sin a – sin b = 2 sin a – b2 cos a + b2;
4) Арифметические свойства предела функции:
Если limx → a f (x) = F и limx → a g(x) = G, то
(4) limx → a( f (x) ⋅ g(x)) = (limx → a f (x)) ⋅ (limx → a g(x)) = F ⋅ G.
Применяем эти правила к нашему пределу. Сначала преобразуем алгебраическое выражение
sin(x + Δx) – sin x.
Для этого применим формулу
(3) sin a – sin b = 2 sin a – b2 cos a + b2.
В нашем случае
a = x + Δx; b = x. Тогда
a – b2 = x + Δx – x2 = Δx2;
a + b2 = x + Δx + x2 = 2x + Δx2 = x + Δx2;
sin(x + Δx) – sin x = 2 sin Δx2 ⋅ cos( x + Δx2 );
sin(x + Δx) – sin xΔx = 2 sin Δx2 ⋅ cos( x + Δx2 )Δx = sin Δx2Δx2 ⋅ cos( x + Δx2 ).
Теперь сделаем подстановку Δx2 = t. При Δx → 0, t → 0. Применим первый замечательный предел (1):
limΔx → 0 sin Δx2Δx2 = limt → 0 sin tt = 1.
Сделаем такую же подстановку Δx2 = t и используем свойство непрерывности (2):
limΔx → 0 cos( x + Δx2 ) = limt → 0 cos( x + t ) = cos x.
Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):
( sin x ) ′ = limΔx → 0 sin(x + Δx) – sin xΔx = limΔx → 0[ sin Δx2Δx2 ⋅ cos( x + Δx2 ) ] =
limΔx → 0[ sin Δx2Δx2 ] ⋅ limΔx → 0[ cos( x + Δx2 ) ] = 1 ⋅ cos x = cos x.
Формула производной синуса доказана.
Примеры
Все примеры Рассмотрим простые примеры нахождения производных от функций, содержащих синус. Мы найдем производные от следующих функций:
y = sin 2x , y = sin 2 x и y = sin 3 x .
Пример 1
Все примерыНайти производную от sin 2x.
Решение
Сначала найдем производную от самой простой части:
( 2x )′ = 2( x )′ = 2 · 1 = 2.
Применяем формулу производной сложной функции.
( sin 2x ) ′ = ( sin u ) ′x = ( sin u ) ′u ⋅ u ′x = cos u ⋅ (2x) ′ = cos 2x ⋅ 2 = 2 cos 2x.
Здесь u = 2x.
Ответ
( sin 2x )′ = 2 cos 2x.
Пример 2
Все примеры Найти производную от синуса в квадрате:
y = sin 2 x.
Решение
Перепишем исходную функцию в более понятном виде:
y = sin 2 x ≡ ( sin x ) 2.
Найдем производную от самой простой части:
( sin x ) ′ = cos x.
Применяем формулу производной сложной функции.
( ( sin x ) 2 ) ′ = ( u 2 ) ′x = ( u 2 ) ′u ⋅ u ′x = 2u 2 – 1 ⋅ (sin x) ′ = 2u 1 ⋅ cos x =
2u ⋅ cos x = 2 sin x ⋅ cos x.
Здесь u = sin x.
Можно применить одну из формул тригонометрии. Тогда
2 sin x ⋅ cos x = sin 2x.
Ответ
( sin 2 x ) ′ = 2 sin x ⋅ cos x = sin 2x.
Пример 3
Все примеры Найти производную от синуса в кубе:
y = sin 3 x.
Производные высших порядков
Заметим, что производную от sin x первого порядка можно выразить через синус следующим образом:
( sin x ) ′ = cos x = sin( x + π2 ).
Найдем производную второго порядка, используя формулу производной сложной функции:
( sin x ) ′′ = ( (sin x) ′ ) ′ = ( sin( x + π2 ) ) ′ = ( sin u ) ′x = ( sin u ) ′u ⋅ u ′x =
sin( u + π2 ) ⋅ ( x + π2 ) ′x = sin( x + π2 + π2 ) ⋅ 1 = sin( x + 2 π2 ).
Здесь u = x + π2.
Теперь мы можем заметить, что дифференцирование sin x приводит к увеличению его аргумента на π2. Тогда производная n-го порядка имеет вид:
(5) ( sin x ) (n) = sin( x + n π2 ).
Докажем это, применяя метод математической индукции.
Мы уже проверили, что при n = 1, формула (5) справедлива.
Предположим, что формула (5) справедлива при некотором значении n = k. Докажем, что из этого следует, что формула (5) выполняется для n = k + 1.
Выпишем формулу (5) при n = k:
( sin x ) (k) = sin( x + k π2 ).
Дифференцируем это уравнение, применяя правило дифференцирования сложной функции:
( sin x ) (k + 1) = ( sin( x + k π2 ) ) ′ = ( sin u ) ′x = ( sin u ) ′u ⋅ u ′x =
sin( u + π2 ) ⋅ ( x + k π2 ) ′x = sin( x + k π2 + π2 ) ⋅ 1 = sin( x + (k + 1) π2 ).
Здесь u = x + k π2.
Итак, мы нашли:
( sin x ) (k + 1) = sin( x + (k + 1) π2 ).
Если подставить k + 1 = n, то эта формула примет вид (5).
Формула доказана.
Автор: Олег Одинцов. Опубликовано: