Производная e в степени x и показательной функции
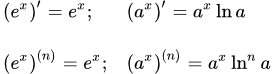
Основные формулы
Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1) ( e x )′ = e x.
Производная показательной функции с основанием степени a равна самой функции, умноженной на натуральный логарифм от a:
(2) ( a x ) ′ = a x ⋅ ln a.
Экспонента – это показательная функция, у которой основание степени равно числу e, которое является следующим пределом:
e = limn → ∞( 1 + 1n ) n ≈ 2, 718281828459045... .
Здесь n может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.
Вывод формулы производной экспоненты
Рассмотрим экспоненту, e в степени x:
y = e x.
Эта функция определена для всех x : –∞ < x < +∞. Найдем ее производную по переменной x. По определению, производная является следующим пределом:
(3) y ′ = limΔx → 0 y(x + Δx) – y(x)Δx = limΔx → 0 e x + Δx – e xΔx.
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам понадобятся следующие факты:
А) Свойство экспоненты:
(4) e a + b = e a ⋅ e b;
Б) Свойство логарифма:
(5) b ln c = ln c b;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6) limx → x0 ln( f (x)) = ln(limx → x0 f (x)).
Здесь f (x) – некоторая функция, у которой существует предел limx → x0 f (x) и этот предел положителен.
Г) Значение второго замечательного предела:
(7) limn → ∞( 1 + 1n ) n = e.
Применяем эти факты к нашему пределу (3). Используем свойство (4):
e x + Δx – e x = e x ⋅ e Δx – e x = e x ( e Δx – 1 );
y ′ = limΔx → 0 e x + Δx – e xΔx = e x limΔx → 0 e Δx – 1Δx.
Сделаем подстановку t = e Δx – 1. Тогда e Δx = t + 1; Δx = ln(t + 1).
В силу непрерывности экспоненты,
limΔx → 0 e Δx = e 0 = 1.
Поэтому при Δx → 0, t → 0. В результате получаем:
y ′ = e x limΔx → 0 e Δx – 1Δx = e x limt → 0 tln(t + 1).
Сделаем подстановку n = 1t. Тогда t = 1n. При t → 0, n → ∞. И мы имеем:
y ′ = e x limt → 0 tln(t + 1) = e x limn → ∞ 1n ln( 1n + 1 ).
Применим свойство логарифма (5):
n ln( 1n + 1 ) = ln( 1n + 1 ) n = ln( 1 + 1n ) n. Тогда
y ′ = e x limn → ∞ 1n ln( 1n + 1 ) = e x limn → ∞ 1ln( 1 + 1n ) n = e x ⋅ 1limn → ∞ ln( 1 + 1n ) n.
Применим свойство (6). Поскольку существует положительный предел limn → ∞( 1n + 1 ) n и логарифм непрерывен, то:
limn → ∞ ln( 1 + 1n ) n = ln limn → ∞( 1 + 1n ) n = ln e = 1.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
y ′ = e x limn → ∞ 1n ln( 1n + 1 ) = e x limn → ∞ 1ln( 1 + 1n ) n = e x ⋅ 1ln e = e x ⋅ 11 = e x.
Тем самым мы получили формулу (1) производной экспоненты.
Вывод формулы производной показательной функции
Теперь выведем формулу (2) производной показательной функции с основанием степени a. Мы считаем, что a > 0 и a ≠ 1. Тогда показательная функция
(8) y = a x
Определена для всех x : –∞ < x < +∞.
Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции и логарифма.
a = e ln a;
a x = ( e ln a ) x = e ln a ⋅ x.
Итак, мы преобразовали формулу (8) к следующему виду:
y = e ln a ⋅ x.
Находим производную. Выносим постоянную ln a за знак производной:
( ln a ⋅ x ) ′ = ln a ⋅ ( x ) ′ = ln a ⋅ 1 = ln a.
Применяем формулу производной сложной функции:
y ′ = ( e ln a ⋅ x ) ′ = ( e u ) ′x = ( e u ) ′u ⋅ u ′x = e u ⋅ ( ln a ⋅ x ) ′ = e ln a ⋅ x ⋅ ln a = a x ⋅ ln a.
Здесь u = ln a ⋅ x.
Тем самым, мы нашли производную показательной функции с произвольным основанием степени:
( a x ) ′ = a x ⋅ ln a.
Другие способы вывода производной экспоненты
Пусть нам известна формула производной натурального логарифма:
(9) ( ln x ) ′ = 1x.
Тогда мы можем вывести формулу производной экспоненты, учитывая, что экспонента является обратной функцией к натуральному логарифму.
Перепишем формулу (9) в следующем виде:
dydx = 1x,
где y = ln x.
Переменные можно обозначать любыми буквами. Поменяем местами x и y:
(10) dxdy = 1y,
где x = ln y.
Теперь рассмотрим экспоненту (e в степени x):
(11) y = e x.
Применим формулу производной обратной функции:
(12) dydx = 1dxdy.
Обратной функцией к экспоненте является натуральный логарифм. Подставим значение производной натурального логарифма (10):
dydx = 1dxdy = 11y = y.
И, наконец, выразим y через x по формуле (11):
y ′ ≡ dydx = y = e x.
Формула доказана.
Теперь докажем формулу производной экспоненты, применяя формулу производной сложной функции. Поскольку функции ln x и e x являются обратными друг к другу, то
ln e x = x.
Дифференцируем это уравнение по переменной x:
(13) ( ln e x ) ′ = (x) ′.
Производная от икса равна единице:
( x ) ′ = ( x 1 ) ′ = 1 ⋅ x 1 – 1 = 1 ⋅ x 0 = 1 ⋅ 1 = 1.
Применим формулу производной сложной функции:
( ln e x ) ′ = ( ln u ) ′u ⋅ u ′x = 1u ⋅ ( e x ) ′ = 1e x ⋅ ( e x ) ′.
Здесь u = e x. Подставим в (13):
1e x ⋅ ( e x ) ′ = 1.
Отсюда
( e x ) ′ = e x.
Пример
Все примеры Найти производные от e в степени 2x, e в степени 3x и e в степени nx. То есть найти производные функций
y = e 2x, y = e 3x и y = e nx.
Решение
Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = e nx. Затем подставим n = 2 и n = 3. И из общей формулы найдем выражения для производных от e 2x, e 3x и e nx.
Итак, имеем исходную функцию
y = e nx.
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции u = nx, зависящей от переменной x: u = u(x);
2) Функции f = e u, зависящей от переменной u: f = f (u).
Тогда исходная функция y(x) составлена из функций f и u:
y(x) = f (u(x)).
Найдем производную от функции u по переменной x:
u ′ = (nx) ′ = n(x) ′ = n ⋅ 1 = n.
Найдем производную от функции f по переменной u:
f ′u = (e u) ′u = e u.
Применяем формулу производной сложной функции.
y ′x = f ′u ⋅ u ′x = e u ⋅ n = e nx ⋅ n = ne nx.
Здесь мы подставили u = nx.
Итак, мы нашли:
( e nx ) ′ = ne nx.
Подставляем n = 2 и n = 3.
Ответ
( e 2x ) ′ = 2e 2x; ( e 3x ) ′ = 3e 3x; ( e nx ) ′ = ne nx.
Производные высших порядков от e в степени x
Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:
(14) y = e x.
Мы нашли ее производную первого порядка:
(1) y ′ = ( e x ) ′ = e x.
Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
y ′′ = ( y ′ ) ′ = ( e x ) ′ = e x;
y ′′′ = ( y ′′ ) ′ = ( e x ) ′ = e x.
Отсюда видно, что производная n-го порядка также равна исходной функции:
y (n) = e x.
Производные высших порядков показательной функции
Теперь рассмотрим показательную функцию с основанием степени a:
y = a x.
Мы нашли ее производную первого порядка:
(15) y ′ = a x ln a.
Дифференцируя (15), получаем производные второго и третьего порядка:
y ′′ = ( y ′ ) ′ = ( a x ln a ) ′ = ( a x ) ′ ln a = a x ln a ⋅ ln a = a x ln 2 a;
y ′′′ = ( y ′′ ) ′ = ( a x ln 2 a ) ′ = ( a x ) ′ ln 2 a = a x ln a ⋅ ln 2 a = a x ln 3 a.
Мы видим, что каждое дифференцирование приводит к умножению исходной функции на ln a. Поэтому производная n-го порядка имеет следующий вид:
y (n) = a x ln n a.
Автор: Олег Одинцов. Опубликовано: