Производная степенной функции (степени и корни)
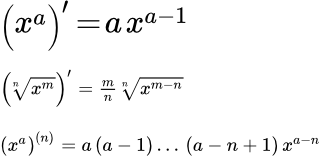
Основные формулы
Производная от x в степени a равна a, умноженному на x в степени a минус один:
(1) .
Производная от корня степени n из x в степени m равна:
(2) .
Вывод формулы производной степенной функции
Случай x > 0
Рассмотрим степенную функцию от переменной x с показателем степени a:
(3) .
Здесь a является произвольным действительным числом. Сначала рассмотрим случай .
Чтобы найти производную функции (3), воспользуемся свойствами степенной функции и преобразуем ее к следующему виду:
.
Теперь находим производную, применяя правило дифференцирования сложной функции:
;
.
Здесь .
Формула (1) доказана.
Вывод формулы производной от корня степени n из x в степени m
Теперь рассмотрим функцию, являющуюся корнем следующего вида:
(4) .
Чтобы найти производную, преобразуем корень к степенной функции:
.
Сравнивая с формулой (3) мы видим, что
.
Тогда
.
По формуле (1) находим производную:
(1) ;
;
(2) .
На практике нет необходимости запоминать формулу (2). Гораздо удобнее сначала преобразовать корни к степенным функциям, а затем находить их производные, применяя формулу (1) (см. примеры в конце страницы).
Случай x = 0
Если , то степенная функция определена и при значении переменной x = 0. Найдем производную функции (3) при x = 0. Для этого воспользуемся определением производной:
.
Подставим x = 0:
.
При этом под производной мы понимаем правосторонний предел, для которого .
Итак, мы нашли:
.
Отсюда видно, что при , .
При , .
При , .
Этот результат получается и по формуле (1):
(1) .
Поэтому формула (1) справедлива и при x = 0.
Случай x < 0
Снова рассмотрим функцию (3):
(3) .
При некоторых значениях постоянной a, она определена и при отрицательных значениях переменной x. А именно, пусть a будет рациональным числом. Тогда его можно представить в виде несократимой дроби:
,
где m и n – целые числа, не имеющие общего делителя.
Если n нечетное, то степенная функция определена и при отрицательных значениях переменной x. Например, при n = 3 и m = 1 мы имеем кубический корень из x:
.
Он определен и при отрицательных значениях переменной x.
Найдем производную степенной функции (3) при и при рациональных значениях постоянной a, для которых она определена. Для этого представим x в следующем виде:
.
Тогда ,
.
Находим производную, вынося постоянную за знак производной и применяя правило дифференцирования сложной функции:
.
Здесь . Но
.
Поскольку , то
.
Тогда
.
То есть формула (1) справедлива и при :
(1) .
Производные высших порядков
Теперь найдем производные высших порядков от степенной функции
(3) .
Производную первого порядка мы уже нашли:
.
Вынося постоянную a за знак производной, находим производную второго порядка:
.
Аналогичным образом находим производные третьего и четвертого порядков:
;
.
Отсюда видно, что производная произвольного n-го порядка имеет следующий вид:
.
Заметим, что если a является натуральным числом, , то n-я производная является постоянной:
.
Тогда все последующие производные равны нулю:
,
при .
Примеры вычисления производных
Пример
Все примеры Найдите производную функции:
.
Решение
Преобразуем корни к степеням:
;
.
Тогда исходная функция приобретает вид:
.
Находим производные степеней:
;
.
Производная постоянной равна нулю:
.
Применяем правило дифференцирования суммы и выносим постоянные за знак производной:
.
Применяем правило дифференцирования сложной функции:
.
Здесь .
Преобразуем степени в корни:
;
;
;
;
;
.
Ответ
Еще примеры
Найти производные следующих функций, зависящих от переменной x:
Решение > > > Решение > > > Решение > > > Решение > > > Решение > > >
Найти производную шестого порядка следующей функции:
.
Решение > > >
Автор: Олег Одинцов. Опубликовано:
