Примеры решений интегралов по частям, содержащих произведение многочлена на sin x, cos x или e^x

Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых является произведением многочлена на экспоненту (е в степени х) или на синус (sin x) или на косинус (cos x).

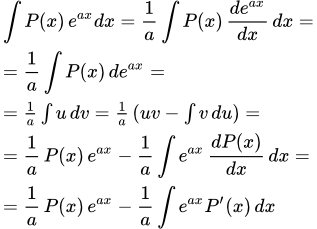
Формула интегрирования по частям

При решении примеров этого раздела, используется формула интегрирования по частям:
;
.
Подробнее >>>

Примеры интегралов, содержащих произведение многочлена и sin x, cos x или e^x

Вот примеры таких интегралов:
,   ,   .

Для интегрирования подобных интегралов, многочлен обозначают через u, а оставшуюся часть – через v dx. Далее применяют формулу интегрирования по частям.

Ниже дается подробное решение этих примеров.

Примеры решения интегралов

Пример с экспонентой, е в степени х

Определить интеграл:
.

Решение

Введем экспоненту под знак дифференциала:
e ^{– x} dx = – e ^{– x} d(–x) = – d(e ^{– x}).

Интегрируем по частям.

здесь
.
Оставшийся интеграл также интегрируем по частям.
.
.
.
Окончательно имеем:
.

Ответ

.

Пример определения интеграла с синусом

Вычислить интеграл:
.

Решение

Введем синус под знак дифференциала:

Интегрируем по частям.

здесь u = x², v = cos(2x+3), du = (x²)′ dx

Оставшийся интеграл также интегрируем по частям. Для этого вводим косинус под знак дифференциала.


здесь u = x, v = sin(2x+3), du = dx

Окончательно имеем:

Ответ

.

Пример произведения многочлена и косинуса

Вычислить интеграл:
.

Решение

Введем косинус под знак дифференциала:

Интегрируем по частям.

здесь u = x² + 3x + 5, v = sin 2x, du = (x² + 3x + 5)′ dx

Вводим синус под знак дифференциала:

Тогда

Последний интеграл интегрируем по частям

здесь u = x, v = cos 2x, du = dx

Окончательно имеем:
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 19-10-2014