Методы решения физико-математических задач

Примеры умножения многочленов столбиком

Пример умножения многочленов столбиком
Подробно разобраны примеры умножения многочленов столбиком.
Содержание
См. также:
Все примеры

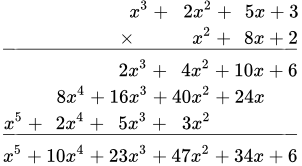
Многочлены можно умножать столбиком тем же способом, что и целые числа. Только старшие разряды, возникающие при умножении чисел с произведением, превышающим 9, не нужно переносить в соседний слева столбец. Далее рассмотрены следующие примеры:
 

Пример 1

Все примеры

Найти произведение многочленов:
.

Решение

Умножаем многочлены столбиком.

1   Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1   Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

2.2   Умножаем следующий член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x.

2.3   Умножаем следующий (старший) член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x.

3   После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x:
;
;
;
.

Заметим, что можно было записывать только коэффициенты, а степени переменной x можно было опустить. Тогда умножение столбиком многочленов будет выглядеть так:

Ответ

.

Пример 2

Все примеры

Найти произведение многочленов столбиком:
.

Решение

При умножении многочленов столбиком важно записывать одинаковые степени переменной x друг под другом. Если некоторые степени x пропущены, то их следует записывать явно, умножив на нуль, либо оставлять пробелы.

В этом примере некоторые степени пропущены. Поэтому запишем их явно, умноженными на нуль:
.
Умножаем многочлены столбиком.

\begin{array}{l} \qquad\qquad\qquad\qquad\quad\;\; x^3+0\cdot x^2-\;\;\, 2x+\;7 \\ \underline{ \qquad\qquad\qquad\qquad\times\quad x^3+\;\;\, 3x^2+0\cdot x-\;5} \\ \qquad\qquad\qquad\qquad\; -5x^3+0\cdot x^2+10x-35 \\ \qquad\quad 3x^5+0\cdot x^4-6x^3+21x^2 \\ \underline{x^6+0\cdot x^5-\;\;\,2x^4+7x^3 \qquad \qquad \qquad \quad \quad\;\;\;} \\ x^6+\;\;3x^5-\;\;\,2x^4-4x^3+21x^2+10x-35 \end{array}

1   Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1   Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

2.2   Следующий член второго многочлена равен нулю. Поэтому его произведение на первый многочлен также равно нулю. Нулевую строку можно не записывать.

2.3   Умножаем следующий член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x.

2.3   Умножаем следующий (старший) член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x.

3   После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x:
.

Более кратко решение можно записать так:

Ответ

.

Автор: Олег Одинцов.     Опубликовано:

См. также:
▲
Меню