Интегрирование дробно-линейной иррациональности

Показано, что интегралы с дробно-линейной иррациональностью (то есть содержащие корни от дробно-линейной функции) сводятся к интегрированию рациональных функций. Разобраны примеры вычисления интегралов с корнями из дробно-линейной функции.

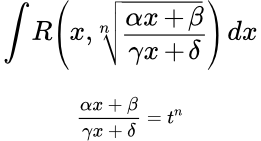
Рассмотрим интегралы с корнем от дробно-линейной функции:
(1)   ,
где R – рациональная функция своих аргументов. То есть функция, составленная из входящих в нее аргументов и произвольных постоянных с помощью конечного числа операций сложения (вычитания), умножения и деления (возведения в целочисленную степень).

Примеры рассматриваемых интегралов с дробно-линейной иррациональностью

Приведем примеры интегралов с корнями вида (1).

Пример 1

Хотя здесь под знаком интеграла входят корни различных степеней, но подынтегральное выражение можно преобразовать следующим образом:
;
;
.

Таким образом, подынтегральное выражение составлено из переменной интегрирования x и корня от линейной функции     с помощью конечного числа операций вычитания, деления и умножения. Поэтому оно является рациональной функцией от x и     и принадлежит рассматриваемому типу (1) со значениями постоянных n = 6, α = β = δ = 1, γ = 0:
.

Пример 2

Здесь мы выполняем преобразование:
.
Отсюда видно, что подынтегральное выражение является рациональной функцией от x и   . Поэтому принадлежит рассматриваемому типу.

Общий пример дробно-линейной иррациональности

В более общем случае, в подынтегральное выражение может входить любое конечное число корней от одной и той же дробно-линейной функции:
(2)   ,
где R – рациональная функция своих аргументов,
  – рациональные числа,
m₁, n₁, ..., m_s, n_s – целые числа.
Действительно, пусть n – общий знаменатель чисел r₁, ..., r_s. Тогда их можно представить в виде:
,
где k₁, k₂, ..., k_s – целые числа. Тогда все входящие в (2) корни являются степенями от   :
,
,
. . . . .
.

То есть все подынтегральное выражение (2) составлено из x и корня     с помощью конечного числа операций сложения, умножения и деления. Поэтому оно является рациональной функцией от x и   :
.

Метод интегрирования корней

Интеграл с дробно-линейной иррациональностью
(1)  
сводится к интегралу от рациональной функции подстановкой
(3)   .

Доказательство

Извлекаем корень степени n из обеих частей (3):
.

Преобразуем (3):
;
;
.

Находим производную:

;
;
.
Дифференциал:
.

Подставляем в (1):
.

Отсюда видно, что подынтегральная функция составлена из постоянных и переменной интегрирования t с помощью конечного числа операций сложения (вычитания), умножения (возведения в целочисленную степень) и деления. Поэтому подынтегральное выражение является рациональной функцией от переменной интегрирования. Таким образом, вычисление интеграла свелось к интегрированию рациональной функции. Что и требовалось доказать.

Пример интегрирования линейной иррациональности

Найти интеграл:

Решение

Поскольку в интеграл входят корни от одной и той же (дробно) линейной функции x + 1, и подынтегральное выражение образовано с помощью операций вычитания и деления, то данный интеграл принадлежит рассматриваемому типу.

Преобразуем подынтегральное выражение, чтобы в него входили корни одной степени:
;
;
.

Делаем подстановку
x + 1 = t ⁶.
Берем дифференциал:
d(x + 1) = dx = ( t ⁶ )′ dt = 6 t ⁵ dt .
Подставляем:
x = t ⁶ – 1;
;
;
.
Выделяем целую часть дроби, замечая что
t ⁶ – 1 = (t – 1)(t ⁵ + t ⁴ + t ³ + t ² + t + 1 ) .
Тогда

.

Ответ

,
где   .

Пример интегрирования дробно-линейной иррациональности

Найти интеграл

Решение

Выделим корень из дробно-линейной функции:
.
Тогда
.
Делаем подстановку
.
Берем дифференциал
.
Находим производную
.
Тогда
.
Далее замечаем, что
.
Подставляем в подынтегральное выражение


.

Ответ

.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 15-12-2014