Методы решения неопределенных интегралов (в картинках)

Приводятся основные сведения о методах вычисления неопределенных интегралов в сжатом виде – в виде изображений. Каждая картинка снабжена заголовком и ссылкой на страницу с подробным изложением метода.
Содержание
Здесь приводятся главные картинки раздела «Методы вычисления неопределенных интегралов». На этих изображениях, в кратком виде представлены главные содержания страниц раздела. На многих из них даются методы решения интегралов. Снизу от каждого изображения имеется заголовок и ссылка на страницу, к которой относится картинка. Просматривая эти картинки, можно освежить в памяти методы вычисления неопределенных интегралов.
Методы вычисления неопределенных интегралов Представлен обзор методов вычисления неопределенных интегралов. Рассмотрены основные методы интегрирования, которые включают в себя интегрирование суммы и разности, вынесение постоянной за знак интеграла, замену переменной, интегрирование по частям. Также рассмотрены специальные методы и приемы интегрирования дробей, корней, тригонометрических и показательных функций. Примеры решений неопределенных интегралов
Представлен обзор методов вычисления неопределенных интегралов. Рассмотрены основные методы интегрирования, которые включают в себя интегрирование суммы и разности, вынесение постоянной за знак интеграла, замену переменной, интегрирование по частям. Также рассмотрены специальные методы и приемы интегрирования дробей, корней, тригонометрических и показательных функций. Примеры решений неопределенных интегралов Здесь представлено 55 примеров решений неопределенных интегралов.
Здесь представлено 55 примеров решений неопределенных интегралов.
 Представлен обзор методов вычисления неопределенных интегралов. Рассмотрены основные методы интегрирования, которые включают в себя интегрирование суммы и разности, вынесение постоянной за знак интеграла, замену переменной, интегрирование по частям. Также рассмотрены специальные методы и приемы интегрирования дробей, корней, тригонометрических и показательных функций. Примеры решений неопределенных интегралов
Представлен обзор методов вычисления неопределенных интегралов. Рассмотрены основные методы интегрирования, которые включают в себя интегрирование суммы и разности, вынесение постоянной за знак интеграла, замену переменной, интегрирование по частям. Также рассмотрены специальные методы и приемы интегрирования дробей, корней, тригонометрических и показательных функций. Примеры решений неопределенных интегралов Здесь представлено 55 примеров решений неопределенных интегралов.
Здесь представлено 55 примеров решений неопределенных интегралов. Основные формулы и методы интегрирования
Основные формулы и методы интегрирования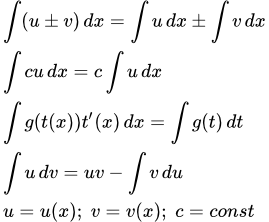 Основные формулы и методы интегрирования. Правило интегрирования суммы или разности. Вынесение постоянной за знак интеграла. Метод замены переменной. Формула интегрирования по частям. Пример решения задачи. Таблица неопределенных интегралов для студентов
Основные формулы и методы интегрирования. Правило интегрирования суммы или разности. Вынесение постоянной за знак интеграла. Метод замены переменной. Формула интегрирования по частям. Пример решения задачи. Таблица неопределенных интегралов для студентов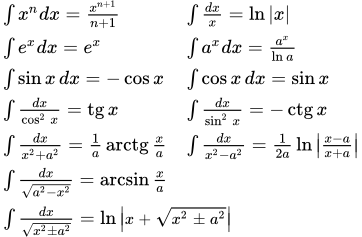 Представлена таблица основных неопределенных интегралов для студентов, а также интегралы, связанные с гиперболическими функциями. Приводится таблица интегралов в дифференциальной форме и основные методы интегрирования. Вычисление неопределенных интегралов от многочленов
Представлена таблица основных неопределенных интегралов для студентов, а также интегралы, связанные с гиперболическими функциями. Приводится таблица интегралов в дифференциальной форме и основные методы интегрирования. Вычисление неопределенных интегралов от многочленов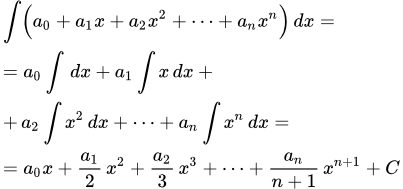 Формула интеграла от многочлена в общем виде. Примеры вычисления интегралов от многочленов и степенных функций, применяя основные методы интегрирования. Интегрирование методом замены переменной
Формула интеграла от многочлена в общем виде. Примеры вычисления интегралов от многочленов и степенных функций, применяя основные методы интегрирования. Интегрирование методом замены переменной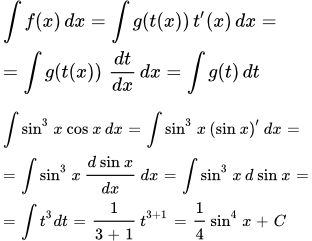 Замена переменной в неопределенном интеграле. Формула преобразования дифференциалов. Примеры интегрирования. Примеры линейных подстановок. Метод интегрирования неопределенного интеграла по частям
Замена переменной в неопределенном интеграле. Формула преобразования дифференциалов. Примеры интегрирования. Примеры линейных подстановок. Метод интегрирования неопределенного интеграла по частям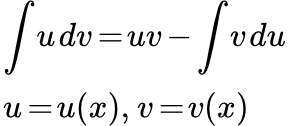 Представлен метод интегрирования неопределенного интеграла по частям. Даны примеры интегралов, вычисляющихся этим методом. Разобраны примеры решений. Примеры решений интегралов по частям, содержащих логарифм и обратные тригонометрические функции
Представлен метод интегрирования неопределенного интеграла по частям. Даны примеры интегралов, вычисляющихся этим методом. Разобраны примеры решений. Примеры решений интегралов по частям, содержащих логарифм и обратные тригонометрические функции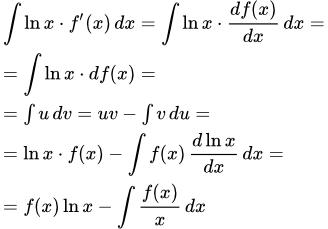 Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых содержит логарифм, арксинус, арктангенс, а также логарифм в целой степени и логарифм от многочлена. Примеры решений интегралов по частям, содержащих произведение многочлена на sin x, cos x или ex
Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых содержит логарифм, арксинус, арктангенс, а также логарифм в целой степени и логарифм от многочлена. Примеры решений интегралов по частям, содержащих произведение многочлена на sin x, cos x или ex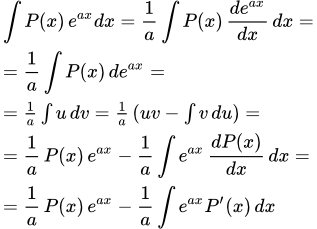 Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых является произведением многочлена на экспоненту (е в степени х) или на синус (sin x) или на косинус (cos x).
Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых является произведением многочлена на экспоненту (е в степени х) или на синус (sin x) или на косинус (cos x).
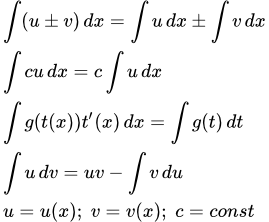 Основные формулы и методы интегрирования. Правило интегрирования суммы или разности. Вынесение постоянной за знак интеграла. Метод замены переменной. Формула интегрирования по частям. Пример решения задачи. Таблица неопределенных интегралов для студентов
Основные формулы и методы интегрирования. Правило интегрирования суммы или разности. Вынесение постоянной за знак интеграла. Метод замены переменной. Формула интегрирования по частям. Пример решения задачи. Таблица неопределенных интегралов для студентов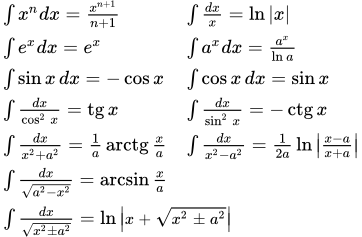 Представлена таблица основных неопределенных интегралов для студентов, а также интегралы, связанные с гиперболическими функциями. Приводится таблица интегралов в дифференциальной форме и основные методы интегрирования. Вычисление неопределенных интегралов от многочленов
Представлена таблица основных неопределенных интегралов для студентов, а также интегралы, связанные с гиперболическими функциями. Приводится таблица интегралов в дифференциальной форме и основные методы интегрирования. Вычисление неопределенных интегралов от многочленов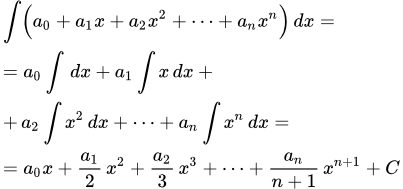 Формула интеграла от многочлена в общем виде. Примеры вычисления интегралов от многочленов и степенных функций, применяя основные методы интегрирования. Интегрирование методом замены переменной
Формула интеграла от многочлена в общем виде. Примеры вычисления интегралов от многочленов и степенных функций, применяя основные методы интегрирования. Интегрирование методом замены переменной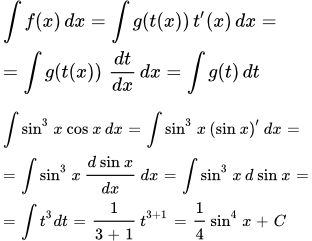 Замена переменной в неопределенном интеграле. Формула преобразования дифференциалов. Примеры интегрирования. Примеры линейных подстановок. Метод интегрирования неопределенного интеграла по частям
Замена переменной в неопределенном интеграле. Формула преобразования дифференциалов. Примеры интегрирования. Примеры линейных подстановок. Метод интегрирования неопределенного интеграла по частям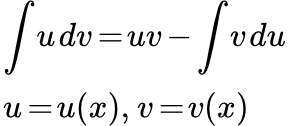 Представлен метод интегрирования неопределенного интеграла по частям. Даны примеры интегралов, вычисляющихся этим методом. Разобраны примеры решений. Примеры решений интегралов по частям, содержащих логарифм и обратные тригонометрические функции
Представлен метод интегрирования неопределенного интеграла по частям. Даны примеры интегралов, вычисляющихся этим методом. Разобраны примеры решений. Примеры решений интегралов по частям, содержащих логарифм и обратные тригонометрические функции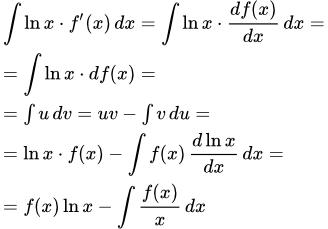 Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых содержит логарифм, арксинус, арктангенс, а также логарифм в целой степени и логарифм от многочлена. Примеры решений интегралов по частям, содержащих произведение многочлена на sin x, cos x или ex
Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых содержит логарифм, арксинус, арктангенс, а также логарифм в целой степени и логарифм от многочлена. Примеры решений интегралов по частям, содержащих произведение многочлена на sin x, cos x или ex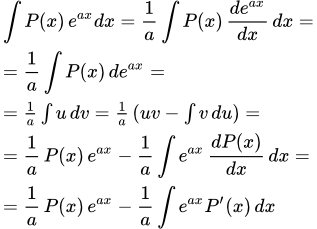 Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых является произведением многочлена на экспоненту (е в степени х) или на синус (sin x) или на косинус (cos x).
Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых является произведением многочлена на экспоненту (е в степени х) или на синус (sin x) или на косинус (cos x). Методы интегрирования рациональных функций (дробей)
Интегрирование рациональных функций (дробей)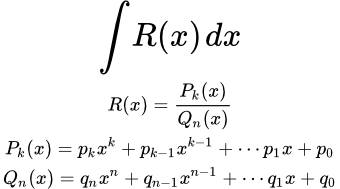 Стандартный метод интегрирования рациональных функций: выделение целой части дроби многочленов, разложение правильной дроби на простейшие, интегрирование простейших дробей. Нестандартные методы интегрирования рациональных функций: применение степенных и дробно-линейных подстановок, интегралы с возвратными многочленами. Примеры умножения многочленов столбиком
Стандартный метод интегрирования рациональных функций: выделение целой части дроби многочленов, разложение правильной дроби на простейшие, интегрирование простейших дробей. Нестандартные методы интегрирования рациональных функций: применение степенных и дробно-линейных подстановок, интегралы с возвратными многочленами. Примеры умножения многочленов столбиком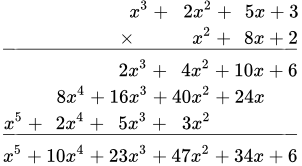 Подробно разобраны примеры умножения многочленов столбиком. Деление многочленов уголком
Подробно разобраны примеры умножения многочленов столбиком. Деление многочленов уголком Приводится доказательство, что неправильную дробь, составленную из многочленов, можно представить в виде суммы многочлена и правильной дроби. Подробно разобраны примеры деления многочленов уголком. Методы разложения многочленов на множители
Приводится доказательство, что неправильную дробь, составленную из многочленов, можно представить в виде суммы многочлена и правильной дроби. Подробно разобраны примеры деления многочленов уголком. Методы разложения многочленов на множители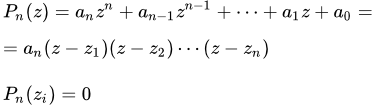 Доказано, что для разложения многочлена на множители, нужно найти его корни. Формулы корней квадратного многочлена. Метод нахождения целых корней. Метод разложения на множители биквадратного многочлена и приводящихся к квадратным. Возвратные многочлены. Примеры разложения многочленов на множители
Доказано, что для разложения многочлена на множители, нужно найти его корни. Формулы корней квадратного многочлена. Метод нахождения целых корней. Метод разложения на множители биквадратного многочлена и приводящихся к квадратным. Возвратные многочлены. Примеры разложения многочленов на множители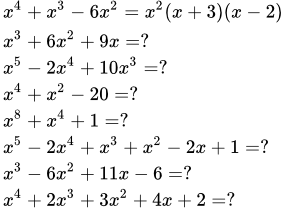 Приводится 8 примеров разложения многочленов на множители. Они включают в себя примеры с решением квадратных и биквадратных уравнений, примеры с возвратными многочленами и примеры с нахождением целых корней у многочленов третьей и четвертой степени. Методы разложения рациональных дробей на простейшие
Приводится 8 примеров разложения многочленов на множители. Они включают в себя примеры с решением квадратных и биквадратных уравнений, примеры с возвратными многочленами и примеры с нахождением целых корней у многочленов третьей и четвертой степени. Методы разложения рациональных дробей на простейшие Приведены наиболее эффективные методы разложения правильных рациональных дробей, составленных из многочленов, на простейшие. Рассмотрены характерные примеры разложения дробей. Интегрирование простейших (элементарных) дробей
Приведены наиболее эффективные методы разложения правильных рациональных дробей, составленных из многочленов, на простейшие. Рассмотрены характерные примеры разложения дробей. Интегрирование простейших (элементарных) дробей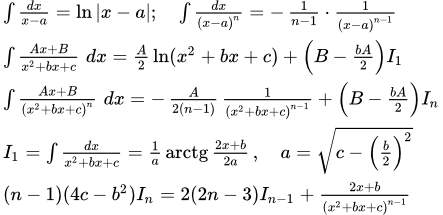 Приводится вывод формул для вычисления интегралов от простейших, элементарных, дробей четырех типов. Более сложные интегралы, от дробей четвертого типа, вычисляются с помощью формулы приведения. Рассмотрен пример интегрирования дроби четвертого типа. Примеры интегрирования рациональных функций (дробей)
Приводится вывод формул для вычисления интегралов от простейших, элементарных, дробей четырех типов. Более сложные интегралы, от дробей четвертого типа, вычисляются с помощью формулы приведения. Рассмотрен пример интегрирования дроби четвертого типа. Примеры интегрирования рациональных функций (дробей)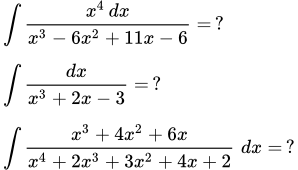 Рассмотрены примеры интегрирования рациональных функций (дробей) с подробными решениями.
Рассмотрены примеры интегрирования рациональных функций (дробей) с подробными решениями.
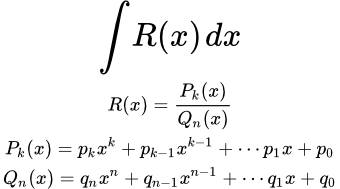 Стандартный метод интегрирования рациональных функций: выделение целой части дроби многочленов, разложение правильной дроби на простейшие, интегрирование простейших дробей. Нестандартные методы интегрирования рациональных функций: применение степенных и дробно-линейных подстановок, интегралы с возвратными многочленами. Примеры умножения многочленов столбиком
Стандартный метод интегрирования рациональных функций: выделение целой части дроби многочленов, разложение правильной дроби на простейшие, интегрирование простейших дробей. Нестандартные методы интегрирования рациональных функций: применение степенных и дробно-линейных подстановок, интегралы с возвратными многочленами. Примеры умножения многочленов столбиком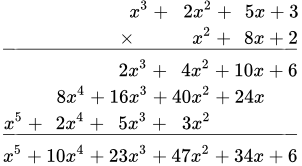 Подробно разобраны примеры умножения многочленов столбиком. Деление многочленов уголком
Подробно разобраны примеры умножения многочленов столбиком. Деление многочленов уголком Приводится доказательство, что неправильную дробь, составленную из многочленов, можно представить в виде суммы многочлена и правильной дроби. Подробно разобраны примеры деления многочленов уголком. Методы разложения многочленов на множители
Приводится доказательство, что неправильную дробь, составленную из многочленов, можно представить в виде суммы многочлена и правильной дроби. Подробно разобраны примеры деления многочленов уголком. Методы разложения многочленов на множители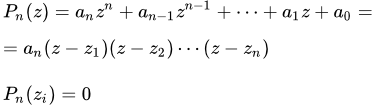 Доказано, что для разложения многочлена на множители, нужно найти его корни. Формулы корней квадратного многочлена. Метод нахождения целых корней. Метод разложения на множители биквадратного многочлена и приводящихся к квадратным. Возвратные многочлены. Примеры разложения многочленов на множители
Доказано, что для разложения многочлена на множители, нужно найти его корни. Формулы корней квадратного многочлена. Метод нахождения целых корней. Метод разложения на множители биквадратного многочлена и приводящихся к квадратным. Возвратные многочлены. Примеры разложения многочленов на множители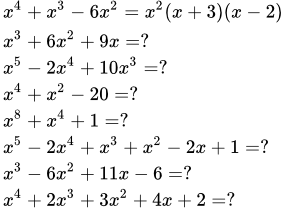 Приводится 8 примеров разложения многочленов на множители. Они включают в себя примеры с решением квадратных и биквадратных уравнений, примеры с возвратными многочленами и примеры с нахождением целых корней у многочленов третьей и четвертой степени. Методы разложения рациональных дробей на простейшие
Приводится 8 примеров разложения многочленов на множители. Они включают в себя примеры с решением квадратных и биквадратных уравнений, примеры с возвратными многочленами и примеры с нахождением целых корней у многочленов третьей и четвертой степени. Методы разложения рациональных дробей на простейшие Приведены наиболее эффективные методы разложения правильных рациональных дробей, составленных из многочленов, на простейшие. Рассмотрены характерные примеры разложения дробей. Интегрирование простейших (элементарных) дробей
Приведены наиболее эффективные методы разложения правильных рациональных дробей, составленных из многочленов, на простейшие. Рассмотрены характерные примеры разложения дробей. Интегрирование простейших (элементарных) дробей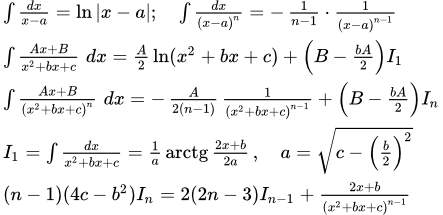 Приводится вывод формул для вычисления интегралов от простейших, элементарных, дробей четырех типов. Более сложные интегралы, от дробей четвертого типа, вычисляются с помощью формулы приведения. Рассмотрен пример интегрирования дроби четвертого типа. Примеры интегрирования рациональных функций (дробей)
Приводится вывод формул для вычисления интегралов от простейших, элементарных, дробей четырех типов. Более сложные интегралы, от дробей четвертого типа, вычисляются с помощью формулы приведения. Рассмотрен пример интегрирования дроби четвертого типа. Примеры интегрирования рациональных функций (дробей)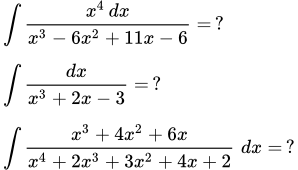 Рассмотрены примеры интегрирования рациональных функций (дробей) с подробными решениями.
Рассмотрены примеры интегрирования рациональных функций (дробей) с подробными решениями. Методы интегрирования иррациональных функций (корней)
Методы интегрирования иррациональных функций (корней)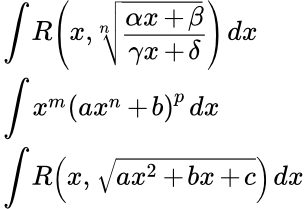 Даны основные методы интегрирования иррациональных функций (корней). Они включают в себя: интегрирование дробно-линейной иррациональности, дифференциального бинома, интегралы с квадратным корнем из квадратного трехчлена. Приводятся тригонометрические подстановки и подстановки Эйлера. Рассмотрены некоторые эллиптические интегралы, выражающиеся через элементарные функции. Интегрирование дробно-линейной иррациональности
Даны основные методы интегрирования иррациональных функций (корней). Они включают в себя: интегрирование дробно-линейной иррациональности, дифференциального бинома, интегралы с квадратным корнем из квадратного трехчлена. Приводятся тригонометрические подстановки и подстановки Эйлера. Рассмотрены некоторые эллиптические интегралы, выражающиеся через элементарные функции. Интегрирование дробно-линейной иррациональности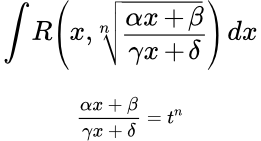 Показано, что интегралы с дробно-линейной иррациональностью (то есть содержащие корни от дробно-линейной функции) сводятся к интегрированию рациональных функций. Разобраны примеры вычисления интегралов с корнями из дробно-линейной функции. Интегрирование дифференциального бинома
Показано, что интегралы с дробно-линейной иррациональностью (то есть содержащие корни от дробно-линейной функции) сводятся к интегрированию рациональных функций. Разобраны примеры вычисления интегралов с корнями из дробно-линейной функции. Интегрирование дифференциального бинома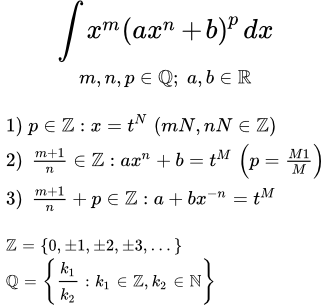 Интегралы от дифференциального бинома сводятся к интегралам от рациональных функций в трех случаях, при определенных соотношениях между показателями степеней. Даны три подстановки, которые приводят к интегралу от рациональной функции. Даны формулы приведения, связывающие интегралы с различными значениями показателей степеней. Подробно разобран пример вычисления интеграла от дифференциального бинома. Вычисление интегралов от многочлена дробь квадратный корень из квадратного трехчлена
Интегралы от дифференциального бинома сводятся к интегралам от рациональных функций в трех случаях, при определенных соотношениях между показателями степеней. Даны три подстановки, которые приводят к интегралу от рациональной функции. Даны формулы приведения, связывающие интегралы с различными значениями показателей степеней. Подробно разобран пример вычисления интеграла от дифференциального бинома. Вычисление интегралов от многочлена дробь квадратный корень из квадратного трехчлена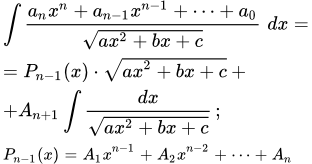 Рассмотрен метод вычисления интеграла от дроби, в числителе которой находится многочлен, а в знаменателе – квадратный корень из трехчлена. Наиболее простым методом вычисления таких интегралов является метод неопределенных коэффициентов. Приведено доказательство применимости этого метода. Разобран пример вычисления такого интеграла. Вычисление интегралов от многочлена дробь степень от двучлена квадратный корень из квадратного трехчлена
Рассмотрен метод вычисления интеграла от дроби, в числителе которой находится многочлен, а в знаменателе – квадратный корень из трехчлена. Наиболее простым методом вычисления таких интегралов является метод неопределенных коэффициентов. Приведено доказательство применимости этого метода. Разобран пример вычисления такого интеграла. Вычисление интегралов от многочлена дробь степень от двучлена квадратный корень из квадратного трехчлена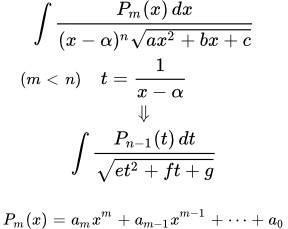 Представлен метод вычисления интегралов, в числителе дроби которых находится многочлен, а в знаменателе – произведение натуральной степени от линейной функции и квадратный корень из квадратного трехчлена. Разобраны примеры вычислений таких интегралов. Вычисление интегралов от двучлена дробь степень от трехчлена квадратный корень из квадратного трехчлена
Представлен метод вычисления интегралов, в числителе дроби которых находится многочлен, а в знаменателе – произведение натуральной степени от линейной функции и квадратный корень из квадратного трехчлена. Разобраны примеры вычислений таких интегралов. Вычисление интегралов от двучлена дробь степень от трехчлена квадратный корень из квадратного трехчлена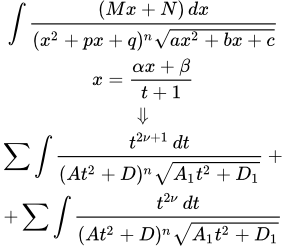 Приводится метод вычисления интегралов, в числителе дроби которых находится линейный двучлен, а в знаменателе – произведение квадратного трехчлена в натуральной степени на квадратный корень из трехчлена. Разобран пример вычисления такого интеграла. Интегрирование рациональной функции от квадратного корня из квадратного трехчлена
Приводится метод вычисления интегралов, в числителе дроби которых находится линейный двучлен, а в знаменателе – произведение квадратного трехчлена в натуральной степени на квадратный корень из трехчлена. Разобран пример вычисления такого интеграла. Интегрирование рациональной функции от квадратного корня из квадратного трехчлена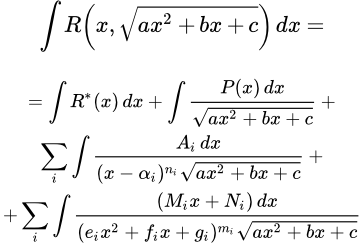 Представлен наиболее эффективный способ интегрирования рациональной функции от квадратного корня из квадратного трехчлена. Разобран пример вычисления такого интеграла. Вычисление интегралов тригонометрическими и гиперболическими подстановками
Представлен наиболее эффективный способ интегрирования рациональной функции от квадратного корня из квадратного трехчлена. Разобран пример вычисления такого интеграла. Вычисление интегралов тригонометрическими и гиперболическими подстановками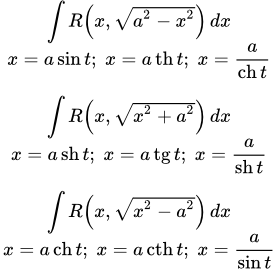 Рассмотрено решение интегралов от рациональной функции с квадратным корнем из квадратного двучлена с помощью тригонометрических и гиперболических подстановок. Даны формулы тригонометрических и гиперболических подстановок и примеры вычисления интегралов. Подстановки Эйлера
Рассмотрено решение интегралов от рациональной функции с квадратным корнем из квадратного двучлена с помощью тригонометрических и гиперболических подстановок. Даны формулы тригонометрических и гиперболических подстановок и примеры вычисления интегралов. Подстановки Эйлера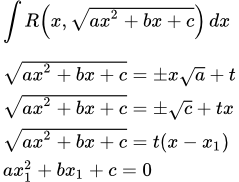 Показано, что интегралы с рациональными функциями от квадратного корня из квадратичного многочлена сводятся к интегралам от рациональных функций с помощью подстановок Эйлера. Даны три подстановки Эйлера и рекомендации по их применению. Разобран пример вычисления интеграла с помощью подстановки Эйлера.
Показано, что интегралы с рациональными функциями от квадратного корня из квадратичного многочлена сводятся к интегралам от рациональных функций с помощью подстановок Эйлера. Даны три подстановки Эйлера и рекомендации по их применению. Разобран пример вычисления интеграла с помощью подстановки Эйлера.
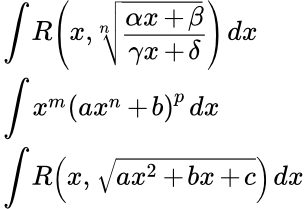 Даны основные методы интегрирования иррациональных функций (корней). Они включают в себя: интегрирование дробно-линейной иррациональности, дифференциального бинома, интегралы с квадратным корнем из квадратного трехчлена. Приводятся тригонометрические подстановки и подстановки Эйлера. Рассмотрены некоторые эллиптические интегралы, выражающиеся через элементарные функции. Интегрирование дробно-линейной иррациональности
Даны основные методы интегрирования иррациональных функций (корней). Они включают в себя: интегрирование дробно-линейной иррациональности, дифференциального бинома, интегралы с квадратным корнем из квадратного трехчлена. Приводятся тригонометрические подстановки и подстановки Эйлера. Рассмотрены некоторые эллиптические интегралы, выражающиеся через элементарные функции. Интегрирование дробно-линейной иррациональности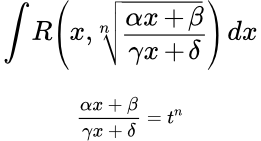 Показано, что интегралы с дробно-линейной иррациональностью (то есть содержащие корни от дробно-линейной функции) сводятся к интегрированию рациональных функций. Разобраны примеры вычисления интегралов с корнями из дробно-линейной функции. Интегрирование дифференциального бинома
Показано, что интегралы с дробно-линейной иррациональностью (то есть содержащие корни от дробно-линейной функции) сводятся к интегрированию рациональных функций. Разобраны примеры вычисления интегралов с корнями из дробно-линейной функции. Интегрирование дифференциального бинома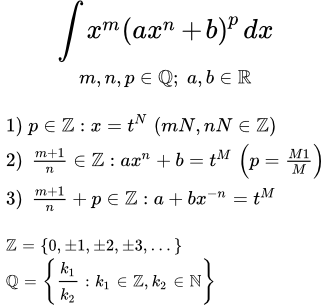 Интегралы от дифференциального бинома сводятся к интегралам от рациональных функций в трех случаях, при определенных соотношениях между показателями степеней. Даны три подстановки, которые приводят к интегралу от рациональной функции. Даны формулы приведения, связывающие интегралы с различными значениями показателей степеней. Подробно разобран пример вычисления интеграла от дифференциального бинома. Вычисление интегралов от многочлена дробь квадратный корень из квадратного трехчлена
Интегралы от дифференциального бинома сводятся к интегралам от рациональных функций в трех случаях, при определенных соотношениях между показателями степеней. Даны три подстановки, которые приводят к интегралу от рациональной функции. Даны формулы приведения, связывающие интегралы с различными значениями показателей степеней. Подробно разобран пример вычисления интеграла от дифференциального бинома. Вычисление интегралов от многочлена дробь квадратный корень из квадратного трехчлена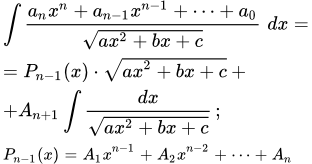 Рассмотрен метод вычисления интеграла от дроби, в числителе которой находится многочлен, а в знаменателе – квадратный корень из трехчлена. Наиболее простым методом вычисления таких интегралов является метод неопределенных коэффициентов. Приведено доказательство применимости этого метода. Разобран пример вычисления такого интеграла. Вычисление интегралов от многочлена дробь степень от двучлена квадратный корень из квадратного трехчлена
Рассмотрен метод вычисления интеграла от дроби, в числителе которой находится многочлен, а в знаменателе – квадратный корень из трехчлена. Наиболее простым методом вычисления таких интегралов является метод неопределенных коэффициентов. Приведено доказательство применимости этого метода. Разобран пример вычисления такого интеграла. Вычисление интегралов от многочлена дробь степень от двучлена квадратный корень из квадратного трехчлена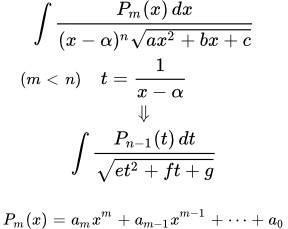 Представлен метод вычисления интегралов, в числителе дроби которых находится многочлен, а в знаменателе – произведение натуральной степени от линейной функции и квадратный корень из квадратного трехчлена. Разобраны примеры вычислений таких интегралов. Вычисление интегралов от двучлена дробь степень от трехчлена квадратный корень из квадратного трехчлена
Представлен метод вычисления интегралов, в числителе дроби которых находится многочлен, а в знаменателе – произведение натуральной степени от линейной функции и квадратный корень из квадратного трехчлена. Разобраны примеры вычислений таких интегралов. Вычисление интегралов от двучлена дробь степень от трехчлена квадратный корень из квадратного трехчлена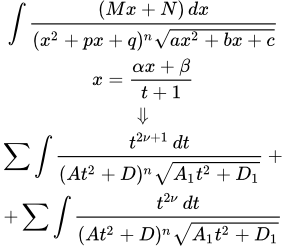 Приводится метод вычисления интегралов, в числителе дроби которых находится линейный двучлен, а в знаменателе – произведение квадратного трехчлена в натуральной степени на квадратный корень из трехчлена. Разобран пример вычисления такого интеграла. Интегрирование рациональной функции от квадратного корня из квадратного трехчлена
Приводится метод вычисления интегралов, в числителе дроби которых находится линейный двучлен, а в знаменателе – произведение квадратного трехчлена в натуральной степени на квадратный корень из трехчлена. Разобран пример вычисления такого интеграла. Интегрирование рациональной функции от квадратного корня из квадратного трехчлена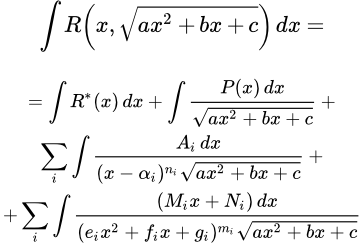 Представлен наиболее эффективный способ интегрирования рациональной функции от квадратного корня из квадратного трехчлена. Разобран пример вычисления такого интеграла. Вычисление интегралов тригонометрическими и гиперболическими подстановками
Представлен наиболее эффективный способ интегрирования рациональной функции от квадратного корня из квадратного трехчлена. Разобран пример вычисления такого интеграла. Вычисление интегралов тригонометрическими и гиперболическими подстановками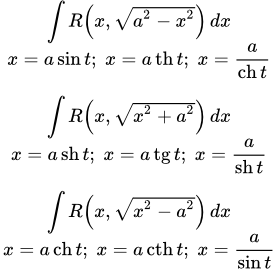 Рассмотрено решение интегралов от рациональной функции с квадратным корнем из квадратного двучлена с помощью тригонометрических и гиперболических подстановок. Даны формулы тригонометрических и гиперболических подстановок и примеры вычисления интегралов. Подстановки Эйлера
Рассмотрено решение интегралов от рациональной функции с квадратным корнем из квадратного двучлена с помощью тригонометрических и гиперболических подстановок. Даны формулы тригонометрических и гиперболических подстановок и примеры вычисления интегралов. Подстановки Эйлера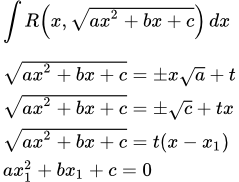 Показано, что интегралы с рациональными функциями от квадратного корня из квадратичного многочлена сводятся к интегралам от рациональных функций с помощью подстановок Эйлера. Даны три подстановки Эйлера и рекомендации по их применению. Разобран пример вычисления интеграла с помощью подстановки Эйлера.
Показано, что интегралы с рациональными функциями от квадратного корня из квадратичного многочлена сводятся к интегралам от рациональных функций с помощью подстановок Эйлера. Даны три подстановки Эйлера и рекомендации по их применению. Разобран пример вычисления интеграла с помощью подстановки Эйлера. Методы интегрирования тригонометрических функций
Методы интегрирования тригонометрических функций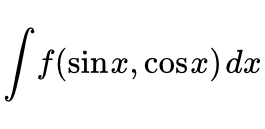 Представлены основные тригонометрические формулы и основные подстановки. Изложены методы интегрирования тригонометрических функций – интегрирование рациональных функций, произведение степенных функций от sin x и cos x, произведение многочлена, экспоненты и синуса или косинуса, интегрирование обратных тригонометрических функций. Затронуты нестандартные методы. Интегрирование тригонометрических рациональных функций
Представлены основные тригонометрические формулы и основные подстановки. Изложены методы интегрирования тригонометрических функций – интегрирование рациональных функций, произведение степенных функций от sin x и cos x, произведение многочлена, экспоненты и синуса или косинуса, интегрирование обратных тригонометрических функций. Затронуты нестандартные методы. Интегрирование тригонометрических рациональных функций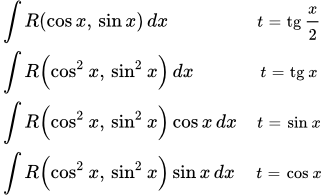 Представлены методы интегрирования тригонометрических рациональных функций. Подробно рассмотрены три примера интегрирования таких функций. Интегрирование произведения степенных функций от sin x и cos x
Представлены методы интегрирования тригонометрических рациональных функций. Подробно рассмотрены три примера интегрирования таких функций. Интегрирование произведения степенных функций от sin x и cos x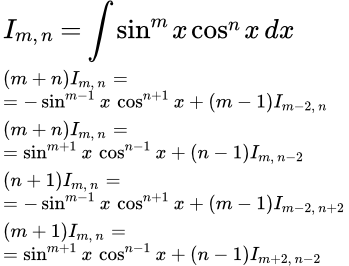 Показано, что интеграл от произведения степенных функций от sin x и cos x можно привести к интегралу от дифференциального бинома. При целых значениях показателей степени, такие интегралы легко вычисляются по частям или с помощью формул приведения. Дан вывод формул приведения. Приводится пример вычисления такого интеграла. Интегрирование произведения многочлена, экспоненты и синуса или косинуса
Показано, что интеграл от произведения степенных функций от sin x и cos x можно привести к интегралу от дифференциального бинома. При целых значениях показателей степени, такие интегралы легко вычисляются по частям или с помощью формул приведения. Дан вывод формул приведения. Приводится пример вычисления такого интеграла. Интегрирование произведения многочлена, экспоненты и синуса или косинуса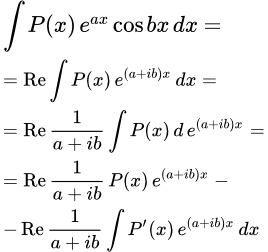 Представлен метод вычисления интегралов, содержащих произведение многочлена, экспоненты и синуса или косинуса. Интегрирование осуществляется с применением формулы Эйлера.
Представлен метод вычисления интегралов, содержащих произведение многочлена, экспоненты и синуса или косинуса. Интегрирование осуществляется с применением формулы Эйлера.
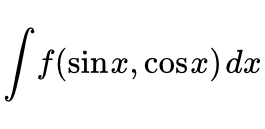 Представлены основные тригонометрические формулы и основные подстановки. Изложены методы интегрирования тригонометрических функций – интегрирование рациональных функций, произведение степенных функций от sin x и cos x, произведение многочлена, экспоненты и синуса или косинуса, интегрирование обратных тригонометрических функций. Затронуты нестандартные методы. Интегрирование тригонометрических рациональных функций
Представлены основные тригонометрические формулы и основные подстановки. Изложены методы интегрирования тригонометрических функций – интегрирование рациональных функций, произведение степенных функций от sin x и cos x, произведение многочлена, экспоненты и синуса или косинуса, интегрирование обратных тригонометрических функций. Затронуты нестандартные методы. Интегрирование тригонометрических рациональных функций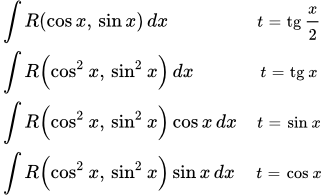 Представлены методы интегрирования тригонометрических рациональных функций. Подробно рассмотрены три примера интегрирования таких функций. Интегрирование произведения степенных функций от sin x и cos x
Представлены методы интегрирования тригонометрических рациональных функций. Подробно рассмотрены три примера интегрирования таких функций. Интегрирование произведения степенных функций от sin x и cos x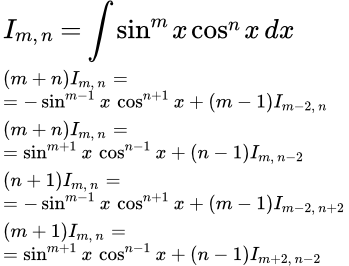 Показано, что интеграл от произведения степенных функций от sin x и cos x можно привести к интегралу от дифференциального бинома. При целых значениях показателей степени, такие интегралы легко вычисляются по частям или с помощью формул приведения. Дан вывод формул приведения. Приводится пример вычисления такого интеграла. Интегрирование произведения многочлена, экспоненты и синуса или косинуса
Показано, что интеграл от произведения степенных функций от sin x и cos x можно привести к интегралу от дифференциального бинома. При целых значениях показателей степени, такие интегралы легко вычисляются по частям или с помощью формул приведения. Дан вывод формул приведения. Приводится пример вычисления такого интеграла. Интегрирование произведения многочлена, экспоненты и синуса или косинуса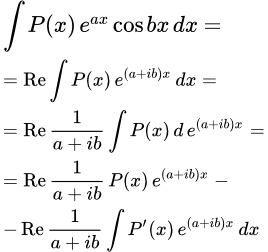 Представлен метод вычисления интегралов, содержащих произведение многочлена, экспоненты и синуса или косинуса. Интегрирование осуществляется с применением формулы Эйлера.
Представлен метод вычисления интегралов, содержащих произведение многочлена, экспоненты и синуса или косинуса. Интегрирование осуществляется с применением формулы Эйлера. 