Производная функции в точке (в картинках)

Приводятся определения, теоремы, свойства и методы вычислений производной функции в точке в сжатом виде – в виде изображений. Каждая картинка снабжена ссылкой на страницу с подробным изложением материала.
Содержание
Далее приводятся главные картинки раздела «Производная функции в точке». На них изображены основные понятия и формулы дифференцирования. Каждое изображение снабжено заголовком, описанием и ссылкой на страницу с подробным изложением материала. Пройдя по этой ссылке можно посмотреть доказательство выбранного правила и примеры его применения. Также, просматривая картинки, можно освежить в памяти основные понятия, связанные с вычислением производных.
Определение производной и основные понятия
Производная функции в точке – определения, теоремы и свойства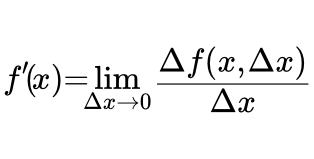 Определения, теоремы и свойства производной и дифференциала функции одной переменной в точке. Методы вычислений и формулы производных элементарных функций. Производные и дифференциалы высших порядков.
Определения, теоремы и свойства производной и дифференциала функции одной переменной в точке. Методы вычислений и формулы производных элементарных функций. Производные и дифференциалы высших порядков. 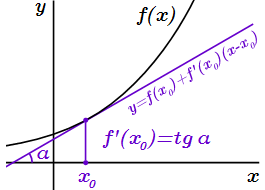 Геометрический смысл производной
Геометрический смысл производной 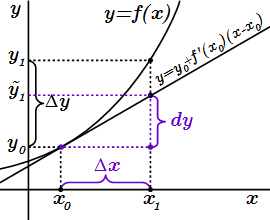 Дифференциал функции в точке x0 – это приращение ординаты касательной, проведенной к графику в этой точке. Примеры решений производных
Дифференциал функции в точке x0 – это приращение ординаты касательной, проведенной к графику в этой точке. Примеры решений производных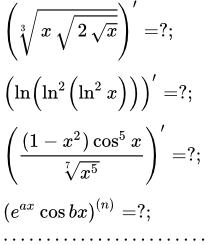 Страница содержит ссылки на 56 примеров решений производных. Физический смысл производной
Страница содержит ссылки на 56 примеров решений производных. Физический смысл производной На примере из механики показывается, что мгновенная скорость движения точки равна производной координаты этой точки по времени. Ускорение равно производной скорости по времени, или второй производной ее координаты по времени. Аналогичным образом, мгновенная скорость изменения любой физической величины равна производной этой величины по времени.
На примере из механики показывается, что мгновенная скорость движения точки равна производной координаты этой точки по времени. Ускорение равно производной скорости по времени, или второй производной ее координаты по времени. Аналогичным образом, мгновенная скорость изменения любой физической величины равна производной этой величины по времени. 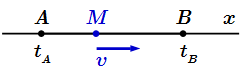 Движение точки M по прямой от A к B. Определение производной функции в точке
Движение точки M по прямой от A к B. Определение производной функции в точке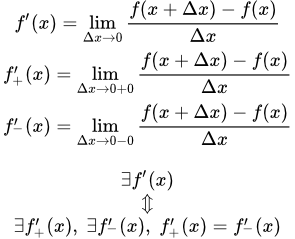 Определение производной функции в точке. Примеры вычисления производных, используя определение. Односторонние производные справа и слева. Лемма об односторонних производных.
Определение производной функции в точке. Примеры вычисления производных, используя определение. Односторонние производные справа и слева. Лемма об односторонних производных. 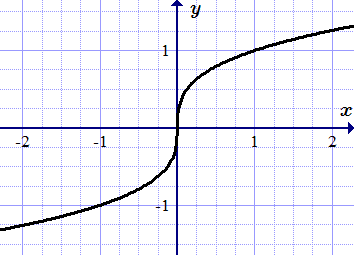 Производная функции в точке x = 0 равна плюс бесконечности.
Производная функции в точке x = 0 равна плюс бесконечности. 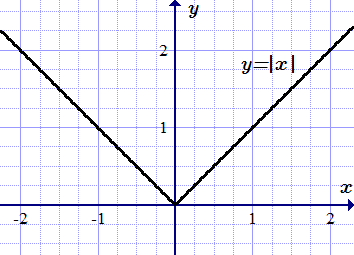 Функция y = |x| не имеет производной в точке x = 0. Дифференцируемые функции в точке – определение и свойства
Функция y = |x| не имеет производной в точке x = 0. Дифференцируемые функции в точке – определение и свойства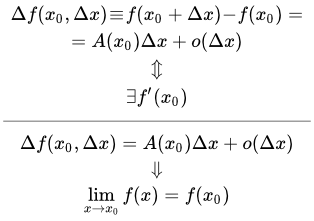 Определение дифференцируемой функции одной переменной в точке. Доказательство теорем о существовании производной и непрерывности дифференцируемой функции. Геометрический смысл производной
Определение дифференцируемой функции одной переменной в точке. Доказательство теорем о существовании производной и непрерывности дифференцируемой функции. Геометрический смысл производной Проведен анализ геометрического смысла производной. Выявлено, что производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в рассматриваемой точке. Рассмотрены случаи, когда производная равна бесконечности.
Проведен анализ геометрического смысла производной. Выявлено, что производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в рассматриваемой точке. Рассмотрены случаи, когда производная равна бесконечности. 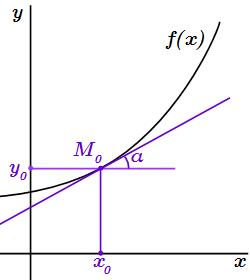 Производная функции в x0 равна тангенсу угла наклона касательной к оси абсцисс: f′(x0) = tg α.
Производная функции в x0 равна тангенсу угла наклона касательной к оси абсцисс: f′(x0) = tg α. 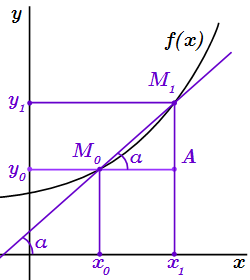 Тангенс угла наклона секущей равен отношению приращения функции к приращению ее аргумента.
Тангенс угла наклона секущей равен отношению приращения функции к приращению ее аргумента. 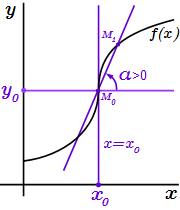 Производная равна плюс бесконечности
Производная равна плюс бесконечности 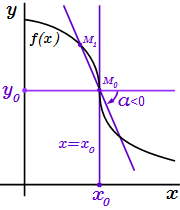 Производная равна минус бесконечности
Производная равна минус бесконечности 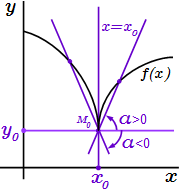 Производная равна бесконечности без определенного знака Касательная и нормаль к графику функции
Производная равна бесконечности без определенного знака Касательная и нормаль к графику функции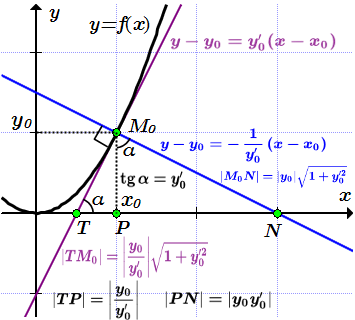 Определения касательной и нормали к графику функции в точке. Определения, подкасательной и поднормали. Угол между двумя кривыми. Примеры решений задач на составление уравнений касательной и нормали, и на вычисление угла между кривыми.
Определения касательной и нормали к графику функции в точке. Определения, подкасательной и поднормали. Угол между двумя кривыми. Примеры решений задач на составление уравнений касательной и нормали, и на вычисление угла между кривыми. 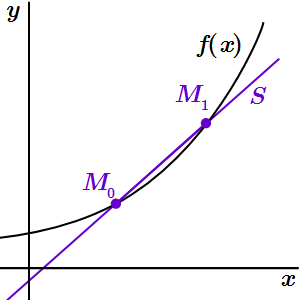 Секущая S пересекает график функции y = f(x) как минимум в двух точках: M0 и M1.
Секущая S пересекает график функции y = f(x) как минимум в двух точках: M0 и M1. 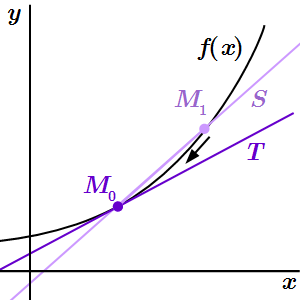 Уравнение касательной T получается из уравнения секущей S при M1 → M0.
Уравнение касательной T получается из уравнения секущей S при M1 → M0. 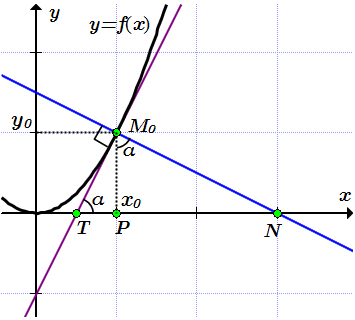 Касательная и нормаль к графику функции y=x2 в точке M0(1;1).
Касательная и нормаль к графику функции y=x2 в точке M0(1;1). 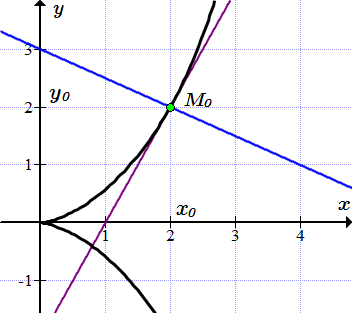 Касательная и нормаль к циссоиде в точке (2;2).
Касательная и нормаль к циссоиде в точке (2;2). 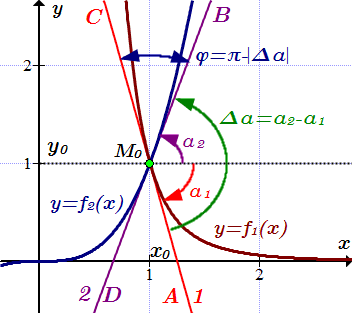 Угол между кривыми равен наименьшему углу между касательными. Производные второго и высших порядков – основные формулы, определения и теоремы
Угол между кривыми равен наименьшему углу между касательными. Производные второго и высших порядков – основные формулы, определения и теоремы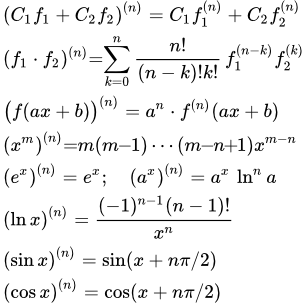 Приводятся определения производных второго и высших порядков и их свойства. Даны формулировки теорем об арифметических свойствах высших производных. Производные второго и третьего порядков сложной функции. Формулы производных высших порядков элементарных функций. Дифференциал функции в точке
Приводятся определения производных второго и высших порядков и их свойства. Даны формулировки теорем об арифметических свойствах высших производных. Производные второго и третьего порядков сложной функции. Формулы производных высших порядков элементарных функций. Дифференциал функции в точке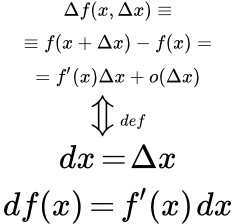 Определение первого дифференциала функции, его смысл и геометрическая интерпретация. Доказательство арифметических свойств и инвариантности его формы. Определение дифференциала высшего порядка, связь с формулой Тейлора. Доказательство не инвариантности его формы. Определение дифференциала второго порядка, обладающего инвариантной формой.
Определение первого дифференциала функции, его смысл и геометрическая интерпретация. Доказательство арифметических свойств и инвариантности его формы. Определение дифференциала высшего порядка, связь с формулой Тейлора. Доказательство не инвариантности его формы. Определение дифференциала второго порядка, обладающего инвариантной формой.  Дифференциал функции в точке x0 – это приращение ординаты касательной, проведенной к графику в этой точке. Примеры как найти дифференциал функции
Дифференциал функции в точке x0 – это приращение ординаты касательной, проведенной к графику в этой точке. Примеры как найти дифференциал функции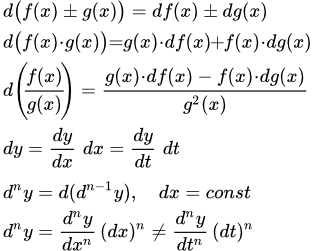 Подробно разобраны примеры вычислений дифференциала функции первого, второго и третьего порядков. Показано как вычислять дифференциалы высших порядков с помощью подстановки. Разобран пример нахождения приближенного значения функции с оценкой погрешности вычисления. Приводятся основные формулы, используемые при решении примеров. Таблица производных элементарных функций
Подробно разобраны примеры вычислений дифференциала функции первого, второго и третьего порядков. Показано как вычислять дифференциалы высших порядков с помощью подстановки. Разобран пример нахождения приближенного значения функции с оценкой погрешности вычисления. Приводятся основные формулы, используемые при решении примеров. Таблица производных элементарных функций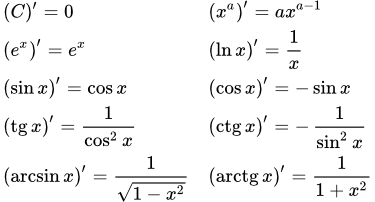 Представлена таблица производных элементарных функций для обучающихся студентов. Приводится таблица производных сложных функций. Даны основные правила дифференцирования.
Представлена таблица производных элементарных функций для обучающихся студентов. Приводится таблица производных сложных функций. Даны основные правила дифференцирования.
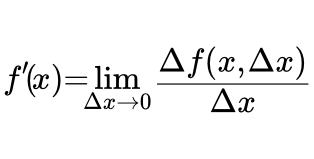 Определения, теоремы и свойства производной и дифференциала функции одной переменной в точке. Методы вычислений и формулы производных элементарных функций. Производные и дифференциалы высших порядков.
Определения, теоремы и свойства производной и дифференциала функции одной переменной в точке. Методы вычислений и формулы производных элементарных функций. Производные и дифференциалы высших порядков.  Геометрический смысл производной
Геометрический смысл производной  Дифференциал функции в точке x0 – это приращение ординаты касательной, проведенной к графику в этой точке. Примеры решений производных
Дифференциал функции в точке x0 – это приращение ординаты касательной, проведенной к графику в этой точке. Примеры решений производных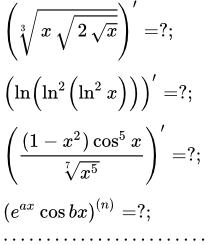 Страница содержит ссылки на 56 примеров решений производных. Физический смысл производной
Страница содержит ссылки на 56 примеров решений производных. Физический смысл производной На примере из механики показывается, что мгновенная скорость движения точки равна производной координаты этой точки по времени. Ускорение равно производной скорости по времени, или второй производной ее координаты по времени. Аналогичным образом, мгновенная скорость изменения любой физической величины равна производной этой величины по времени.
На примере из механики показывается, что мгновенная скорость движения точки равна производной координаты этой точки по времени. Ускорение равно производной скорости по времени, или второй производной ее координаты по времени. Аналогичным образом, мгновенная скорость изменения любой физической величины равна производной этой величины по времени. 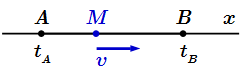 Движение точки M по прямой от A к B. Определение производной функции в точке
Движение точки M по прямой от A к B. Определение производной функции в точке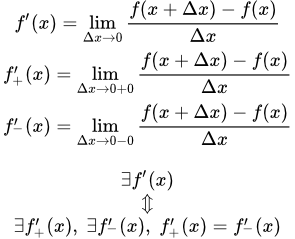 Определение производной функции в точке. Примеры вычисления производных, используя определение. Односторонние производные справа и слева. Лемма об односторонних производных.
Определение производной функции в точке. Примеры вычисления производных, используя определение. Односторонние производные справа и слева. Лемма об односторонних производных.  Производная функции в точке x = 0 равна плюс бесконечности.
Производная функции в точке x = 0 равна плюс бесконечности.  Функция y = |x| не имеет производной в точке x = 0. Дифференцируемые функции в точке – определение и свойства
Функция y = |x| не имеет производной в точке x = 0. Дифференцируемые функции в точке – определение и свойства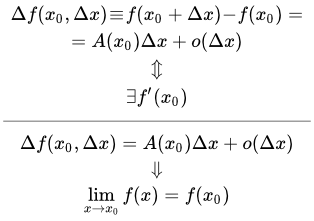 Определение дифференцируемой функции одной переменной в точке. Доказательство теорем о существовании производной и непрерывности дифференцируемой функции. Геометрический смысл производной
Определение дифференцируемой функции одной переменной в точке. Доказательство теорем о существовании производной и непрерывности дифференцируемой функции. Геометрический смысл производной Проведен анализ геометрического смысла производной. Выявлено, что производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в рассматриваемой точке. Рассмотрены случаи, когда производная равна бесконечности.
Проведен анализ геометрического смысла производной. Выявлено, что производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в рассматриваемой точке. Рассмотрены случаи, когда производная равна бесконечности.  Производная функции в x0 равна тангенсу угла наклона касательной к оси абсцисс: f′(x0) = tg α.
Производная функции в x0 равна тангенсу угла наклона касательной к оси абсцисс: f′(x0) = tg α.  Тангенс угла наклона секущей равен отношению приращения функции к приращению ее аргумента.
Тангенс угла наклона секущей равен отношению приращения функции к приращению ее аргумента.  Производная равна плюс бесконечности
Производная равна плюс бесконечности  Производная равна минус бесконечности
Производная равна минус бесконечности  Производная равна бесконечности без определенного знака Касательная и нормаль к графику функции
Производная равна бесконечности без определенного знака Касательная и нормаль к графику функции Определения касательной и нормали к графику функции в точке. Определения, подкасательной и поднормали. Угол между двумя кривыми. Примеры решений задач на составление уравнений касательной и нормали, и на вычисление угла между кривыми.
Определения касательной и нормали к графику функции в точке. Определения, подкасательной и поднормали. Угол между двумя кривыми. Примеры решений задач на составление уравнений касательной и нормали, и на вычисление угла между кривыми.  Секущая S пересекает график функции y = f(x) как минимум в двух точках: M0 и M1.
Секущая S пересекает график функции y = f(x) как минимум в двух точках: M0 и M1.  Уравнение касательной T получается из уравнения секущей S при M1 → M0.
Уравнение касательной T получается из уравнения секущей S при M1 → M0. 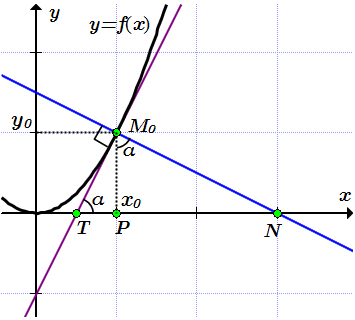 Касательная и нормаль к графику функции y=x2 в точке M0(1;1).
Касательная и нормаль к графику функции y=x2 в точке M0(1;1).  Касательная и нормаль к циссоиде в точке (2;2).
Касательная и нормаль к циссоиде в точке (2;2).  Угол между кривыми равен наименьшему углу между касательными. Производные второго и высших порядков – основные формулы, определения и теоремы
Угол между кривыми равен наименьшему углу между касательными. Производные второго и высших порядков – основные формулы, определения и теоремы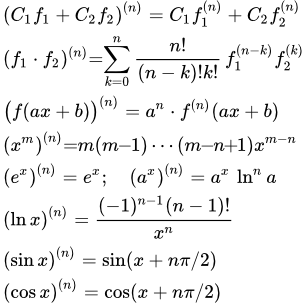 Приводятся определения производных второго и высших порядков и их свойства. Даны формулировки теорем об арифметических свойствах высших производных. Производные второго и третьего порядков сложной функции. Формулы производных высших порядков элементарных функций. Дифференциал функции в точке
Приводятся определения производных второго и высших порядков и их свойства. Даны формулировки теорем об арифметических свойствах высших производных. Производные второго и третьего порядков сложной функции. Формулы производных высших порядков элементарных функций. Дифференциал функции в точке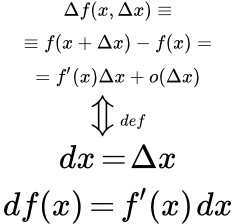 Определение первого дифференциала функции, его смысл и геометрическая интерпретация. Доказательство арифметических свойств и инвариантности его формы. Определение дифференциала высшего порядка, связь с формулой Тейлора. Доказательство не инвариантности его формы. Определение дифференциала второго порядка, обладающего инвариантной формой.
Определение первого дифференциала функции, его смысл и геометрическая интерпретация. Доказательство арифметических свойств и инвариантности его формы. Определение дифференциала высшего порядка, связь с формулой Тейлора. Доказательство не инвариантности его формы. Определение дифференциала второго порядка, обладающего инвариантной формой.  Дифференциал функции в точке x0 – это приращение ординаты касательной, проведенной к графику в этой точке. Примеры как найти дифференциал функции
Дифференциал функции в точке x0 – это приращение ординаты касательной, проведенной к графику в этой точке. Примеры как найти дифференциал функции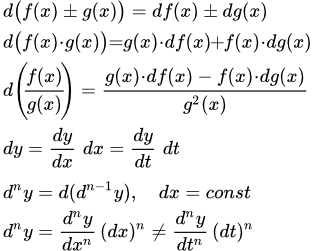 Подробно разобраны примеры вычислений дифференциала функции первого, второго и третьего порядков. Показано как вычислять дифференциалы высших порядков с помощью подстановки. Разобран пример нахождения приближенного значения функции с оценкой погрешности вычисления. Приводятся основные формулы, используемые при решении примеров. Таблица производных элементарных функций
Подробно разобраны примеры вычислений дифференциала функции первого, второго и третьего порядков. Показано как вычислять дифференциалы высших порядков с помощью подстановки. Разобран пример нахождения приближенного значения функции с оценкой погрешности вычисления. Приводятся основные формулы, используемые при решении примеров. Таблица производных элементарных функций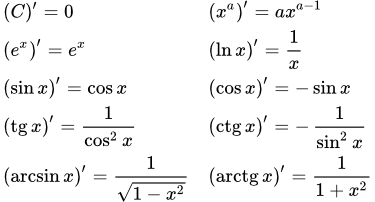 Представлена таблица производных элементарных функций для обучающихся студентов. Приводится таблица производных сложных функций. Даны основные правила дифференцирования.
Представлена таблица производных элементарных функций для обучающихся студентов. Приводится таблица производных сложных функций. Даны основные правила дифференцирования. Методы вычисления производных
Правила дифференцирования - основные формулы вычисления производных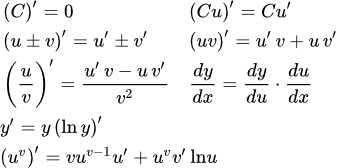 В кратком виде даны правила дифференцирования (формулы вычисления производных). Ссылки на страницы с подробным описанием выбранного правила. Производная постоянной функции (константы)
В кратком виде даны правила дифференцирования (формулы вычисления производных). Ссылки на страницы с подробным описанием выбранного правила. Производная постоянной функции (константы)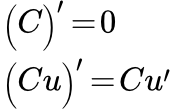 Производная постоянной (константы). Вынесение постоянной за знак производной. Примеры вычисления производных. Пример вычисления производной от функции, составленной из корней. Производная суммы и разности функций
Производная постоянной (константы). Вынесение постоянной за знак производной. Примеры вычисления производных. Пример вычисления производной от функции, составленной из корней. Производная суммы и разности функций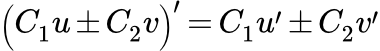 Приведена формула производной суммы и разности функций. Приведено доказательство и подробно разобраны примеры применения этой формулы. Производная произведения двух функций
Приведена формула производной суммы и разности функций. Приведено доказательство и подробно разобраны примеры применения этой формулы. Производная произведения двух функций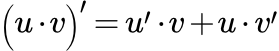 Формула производной произведения двух функций. Доказательство и подробно разобранные примеры применения этой формулы. Формула Лейбница для n-й производной произведения двух функций
Формула производной произведения двух функций. Доказательство и подробно разобранные примеры применения этой формулы. Формула Лейбница для n-й производной произведения двух функций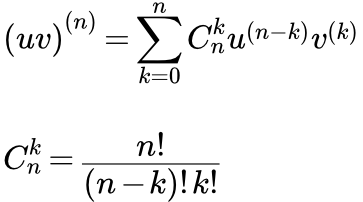 Приводится формула Лейбница для вычисления n-й производной произведения двух функций. Дано ее доказательство двумя способами. Рассмотрен пример вычисления производной n-го порядка. Производная дроби из двух функций
Приводится формула Лейбница для вычисления n-й производной произведения двух функций. Дано ее доказательство двумя способами. Рассмотрен пример вычисления производной n-го порядка. Производная дроби из двух функций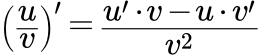 Формула производной дроби из двух функций. Доказательство двумя способами. Подробно разобранные примеры дифференцирования частного. Доказательство формулы производной сложной функции
Формула производной дроби из двух функций. Доказательство двумя способами. Подробно разобранные примеры дифференцирования частного. Доказательство формулы производной сложной функции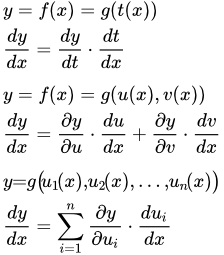 Приводится доказательство формулы производной сложной функции. Подробно рассмотрены случаи, когда сложная функция зависит от одной и двух переменных. Производится обобщение на случай произвольного числа переменных. Примеры применения формулы производной сложной функции
Приводится доказательство формулы производной сложной функции. Подробно рассмотрены случаи, когда сложная функция зависит от одной и двух переменных. Производится обобщение на случай произвольного числа переменных. Примеры применения формулы производной сложной функции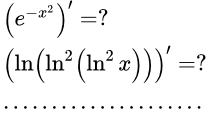 Приводятся примеры вычисления производных сложных функций. Теорема о производной обратной функции
Приводятся примеры вычисления производных сложных функций. Теорема о производной обратной функции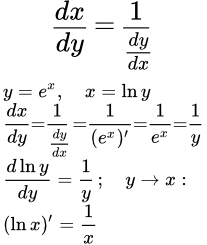 Приводится доказательство теоремы о производной обратной функции. Приводятся примеры применения этой теоремы.
Приводится доказательство теоремы о производной обратной функции. Приводятся примеры применения этой теоремы. 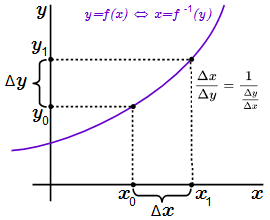 Приращения переменных, связанных строго монотонной функцией f. Вычисление производных с помощью логарифмической производной
Приращения переменных, связанных строго монотонной функцией f. Вычисление производных с помощью логарифмической производной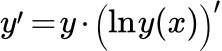 Приводятся примеры вычисления производных с помощью логарифмической производной. Вычисление производных степенно-показательных функций
Приводятся примеры вычисления производных с помощью логарифмической производной. Вычисление производных степенно-показательных функций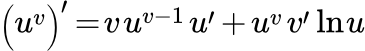 Определение степенно-показательной функции. Вывод формулы для вычисления ее производной. Подробно разобраны примеры вычисления производных степенно-показательных функций. Примеры как найти производные второго и высших порядков
Определение степенно-показательной функции. Вывод формулы для вычисления ее производной. Подробно разобраны примеры вычисления производных степенно-показательных функций. Примеры как найти производные второго и высших порядков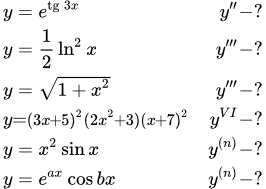 Приводится список применяемых правил для нахождения производных высших порядков. Указаны методы, сокращающие вычисления. Рассмотрены примеры вычисления производных высших порядков явных функций.
Приводится список применяемых правил для нахождения производных высших порядков. Указаны методы, сокращающие вычисления. Рассмотрены примеры вычисления производных высших порядков явных функций. 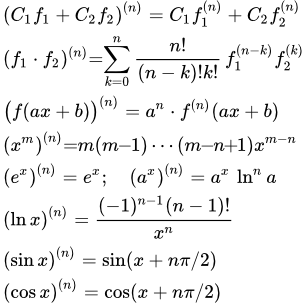 Основные формулы, применяемые для вычисления высших производных. Производная функции, заданной параметрическим способом
Основные формулы, применяемые для вычисления высших производных. Производная функции, заданной параметрическим способом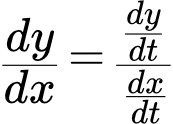 Формула производной функции, заданной параметрическим способом. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка. Производная функции, заданной неявно
Формула производной функции, заданной параметрическим способом. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка. Производная функции, заданной неявно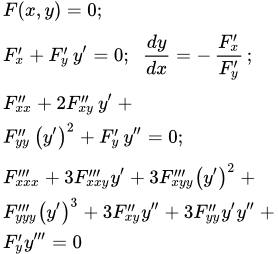 Формула производной функции, заданной неявно. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка.
Формула производной функции, заданной неявно. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка.
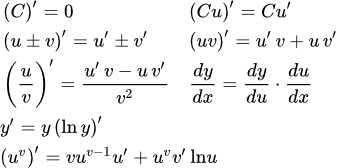 В кратком виде даны правила дифференцирования (формулы вычисления производных). Ссылки на страницы с подробным описанием выбранного правила. Производная постоянной функции (константы)
В кратком виде даны правила дифференцирования (формулы вычисления производных). Ссылки на страницы с подробным описанием выбранного правила. Производная постоянной функции (константы)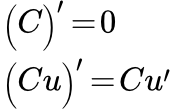 Производная постоянной (константы). Вынесение постоянной за знак производной. Примеры вычисления производных. Пример вычисления производной от функции, составленной из корней. Производная суммы и разности функций
Производная постоянной (константы). Вынесение постоянной за знак производной. Примеры вычисления производных. Пример вычисления производной от функции, составленной из корней. Производная суммы и разности функций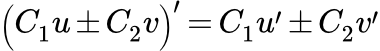 Приведена формула производной суммы и разности функций. Приведено доказательство и подробно разобраны примеры применения этой формулы. Производная произведения двух функций
Приведена формула производной суммы и разности функций. Приведено доказательство и подробно разобраны примеры применения этой формулы. Производная произведения двух функций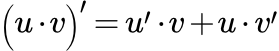 Формула производной произведения двух функций. Доказательство и подробно разобранные примеры применения этой формулы. Формула Лейбница для n-й производной произведения двух функций
Формула производной произведения двух функций. Доказательство и подробно разобранные примеры применения этой формулы. Формула Лейбница для n-й производной произведения двух функций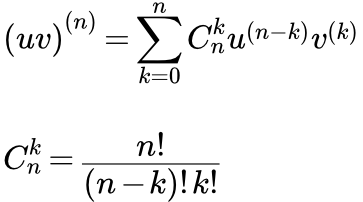 Приводится формула Лейбница для вычисления n-й производной произведения двух функций. Дано ее доказательство двумя способами. Рассмотрен пример вычисления производной n-го порядка. Производная дроби из двух функций
Приводится формула Лейбница для вычисления n-й производной произведения двух функций. Дано ее доказательство двумя способами. Рассмотрен пример вычисления производной n-го порядка. Производная дроби из двух функций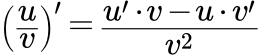 Формула производной дроби из двух функций. Доказательство двумя способами. Подробно разобранные примеры дифференцирования частного. Доказательство формулы производной сложной функции
Формула производной дроби из двух функций. Доказательство двумя способами. Подробно разобранные примеры дифференцирования частного. Доказательство формулы производной сложной функции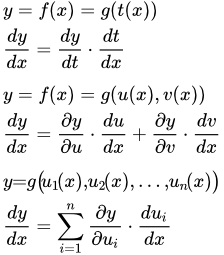 Приводится доказательство формулы производной сложной функции. Подробно рассмотрены случаи, когда сложная функция зависит от одной и двух переменных. Производится обобщение на случай произвольного числа переменных. Примеры применения формулы производной сложной функции
Приводится доказательство формулы производной сложной функции. Подробно рассмотрены случаи, когда сложная функция зависит от одной и двух переменных. Производится обобщение на случай произвольного числа переменных. Примеры применения формулы производной сложной функции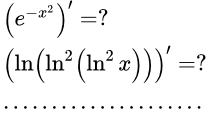 Приводятся примеры вычисления производных сложных функций. Теорема о производной обратной функции
Приводятся примеры вычисления производных сложных функций. Теорема о производной обратной функции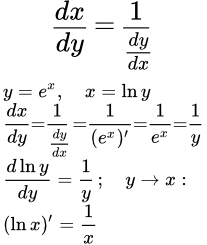 Приводится доказательство теоремы о производной обратной функции. Приводятся примеры применения этой теоремы.
Приводится доказательство теоремы о производной обратной функции. Приводятся примеры применения этой теоремы.  Приращения переменных, связанных строго монотонной функцией f. Вычисление производных с помощью логарифмической производной
Приращения переменных, связанных строго монотонной функцией f. Вычисление производных с помощью логарифмической производной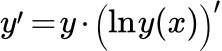 Приводятся примеры вычисления производных с помощью логарифмической производной. Вычисление производных степенно-показательных функций
Приводятся примеры вычисления производных с помощью логарифмической производной. Вычисление производных степенно-показательных функций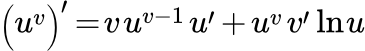 Определение степенно-показательной функции. Вывод формулы для вычисления ее производной. Подробно разобраны примеры вычисления производных степенно-показательных функций. Примеры как найти производные второго и высших порядков
Определение степенно-показательной функции. Вывод формулы для вычисления ее производной. Подробно разобраны примеры вычисления производных степенно-показательных функций. Примеры как найти производные второго и высших порядков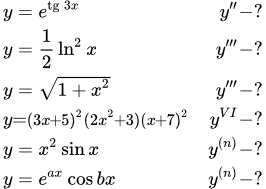 Приводится список применяемых правил для нахождения производных высших порядков. Указаны методы, сокращающие вычисления. Рассмотрены примеры вычисления производных высших порядков явных функций.
Приводится список применяемых правил для нахождения производных высших порядков. Указаны методы, сокращающие вычисления. Рассмотрены примеры вычисления производных высших порядков явных функций. 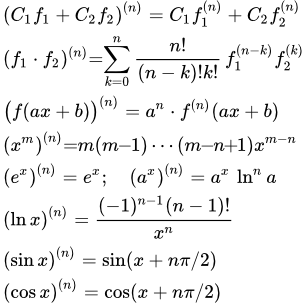 Основные формулы, применяемые для вычисления высших производных. Производная функции, заданной параметрическим способом
Основные формулы, применяемые для вычисления высших производных. Производная функции, заданной параметрическим способом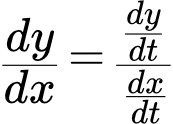 Формула производной функции, заданной параметрическим способом. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка. Производная функции, заданной неявно
Формула производной функции, заданной параметрическим способом. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка. Производная функции, заданной неявно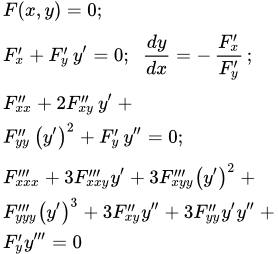 Формула производной функции, заданной неявно. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка.
Формула производной функции, заданной неявно. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка. Производные элементарных функций (вывод формул)
Производные основных элементарных функций и их вывод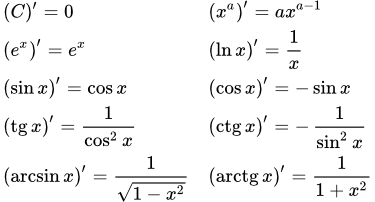 Представлены производные основных элементарных функций и ссылки на страницы с их выводом. Даны формулы производных высших порядков. Производные элементарных функций. Доказательство теоремы
Представлены производные основных элементарных функций и ссылки на страницы с их выводом. Даны формулы производных высших порядков. Производные элементарных функций. Доказательство теоремы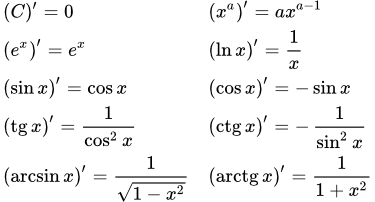 Доказательство теоремы о производных элементарных функций. Доказательство основывается на методах вычисления пределов функций и правилах дифференцирования. Производная натурального логарифма и логарифма по основанию a
Доказательство теоремы о производных элементарных функций. Доказательство основывается на методах вычисления пределов функций и правилах дифференцирования. Производная натурального логарифма и логарифма по основанию a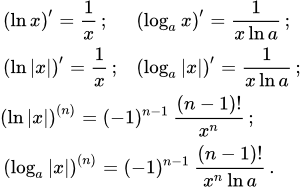 Доказательство и вывод формул производной натурального логарифма и логарифма по основанию a. Примеры вычисления производных от ln 2x, ln 3x и ln nx. Доказательство формулы производной логарифма n-го порядка методом математической индукции. Производная e в степени x и показательной функции
Доказательство и вывод формул производной натурального логарифма и логарифма по основанию a. Примеры вычисления производных от ln 2x, ln 3x и ln nx. Доказательство формулы производной логарифма n-го порядка методом математической индукции. Производная e в степени x и показательной функции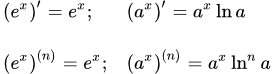 Доказательство и вывод формул производной экспоненты (e в степени x) и показательной функции (a в степени x). Примеры вычисления производных от e^2x, e^3x и e^nx. Формулы производных высших порядков. Производная степенной функции (степени и корни)
Доказательство и вывод формул производной экспоненты (e в степени x) и показательной функции (a в степени x). Примеры вычисления производных от e^2x, e^3x и e^nx. Формулы производных высших порядков. Производная степенной функции (степени и корни)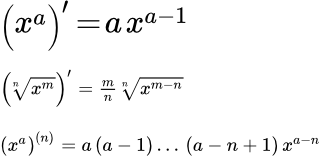 Вывод формулы производной степенной функции (x в степени a). Рассмотрены производные от корней из x. Формула производной степенной функции высшего порядка. Примеры вычисления производных. Производные тригонометрических функций
Вывод формулы производной степенной функции (x в степени a). Рассмотрены производные от корней из x. Формула производной степенной функции высшего порядка. Примеры вычисления производных. Производные тригонометрических функций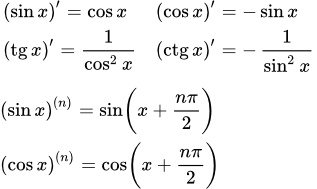 Представлены производные тригонометрических функций. Доказательство и вывод формул. Производные высшего порядка для синуса и косинуса. Производная синуса: (sin x)′
Представлены производные тригонометрических функций. Доказательство и вывод формул. Производные высшего порядка для синуса и косинуса. Производная синуса: (sin x)′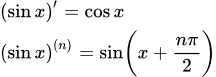 Представлено доказательство и вывод формулы для производной синуса - sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка. Производная косинуса: (cos x)′
Представлено доказательство и вывод формулы для производной синуса - sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка. Производная косинуса: (cos x)′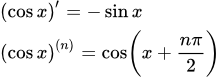 Представлено доказательство и вывод формулы для производной косинуса - cos(x). Примеры вычисления производных от cos 2x, cos 3x, cos nx, косинуса в квадрате, в кубе и в степени n. Формула производной косинуса n-го порядка. Производная тангенса: (tg x)′
Представлено доказательство и вывод формулы для производной косинуса - cos(x). Примеры вычисления производных от cos 2x, cos 3x, cos nx, косинуса в квадрате, в кубе и в степени n. Формула производной косинуса n-го порядка. Производная тангенса: (tg x)′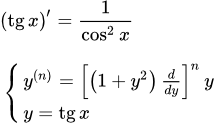 Представлен вывод формулы для производной тангенса - tg(x). Примеры вычисления производных от tg 2x, tg 3x и tg nx. Производная тангенса n-го порядка в виде многочлена по степеням tg(x). Производная котангенса: (ctg x)′
Представлен вывод формулы для производной тангенса - tg(x). Примеры вычисления производных от tg 2x, tg 3x и tg nx. Производная тангенса n-го порядка в виде многочлена по степеням tg(x). Производная котангенса: (ctg x)′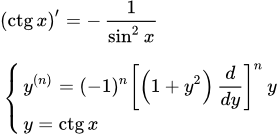 Представлен вывод формулы для производной котангенса - ctg(x). Дана формула производной котангенса n-го порядка в виде многочлена по степеням ctg(x). Коэффициенты этого многочлена связаны рекуррентным соотношением. Вывод производных обратных тригонометрических функций
Представлен вывод формулы для производной котангенса - ctg(x). Дана формула производной котангенса n-го порядка в виде многочлена по степеням ctg(x). Коэффициенты этого многочлена связаны рекуррентным соотношением. Вывод производных обратных тригонометрических функций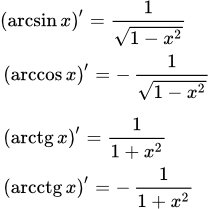 Представлены производные обратных тригонометрических функций и вывод их формул. Также даны выражения производных высших порядков. Ссылки на страницы с более подробным изложением вывода формул. Вывод производных арксинуса (arcsin x)′ и арккосинуса (arccos x)′
Представлены производные обратных тригонометрических функций и вывод их формул. Также даны выражения производных высших порядков. Ссылки на страницы с более подробным изложением вывода формул. Вывод производных арксинуса (arcsin x)′ и арккосинуса (arccos x)′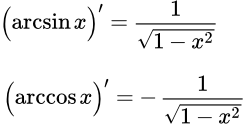 Представлен вывод производных первого порядка арксинуса (arcsin x)′ и арккосинуса (arccos x)′. Для каждой из функций, вывод дан двумя способами. Вывод производных высших порядков арксинуса (arcsin x) и арккосинуса (arccos x)
Представлен вывод производных первого порядка арксинуса (arcsin x)′ и арккосинуса (arccos x)′. Для каждой из функций, вывод дан двумя способами. Вывод производных высших порядков арксинуса (arcsin x) и арккосинуса (arccos x)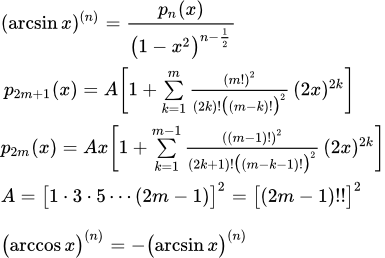 Представлен вывод производных высших порядков арксинуса (arcsin x). Формулы производных арксинуса второго, третьего, четвертого и пятого порядка. Производная n-го порядка выражается через многочлен и корень. Даны уравнения для многочленов и вывод значений их коэффициентов. Выражение производной n-го порядка арккосинуса через производную арксинуса. Вывод производных арктангенса (arctg x)′ и арккотангенса (arcctg x)′
Представлен вывод производных высших порядков арксинуса (arcsin x). Формулы производных арксинуса второго, третьего, четвертого и пятого порядка. Производная n-го порядка выражается через многочлен и корень. Даны уравнения для многочленов и вывод значений их коэффициентов. Выражение производной n-го порядка арккосинуса через производную арксинуса. Вывод производных арктангенса (arctg x)′ и арккотангенса (arcctg x)′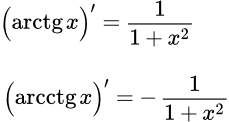 Представлен вывод производных первого порядка арктангенса (arctg x)′ и арккотангенса (arcctg x)′. Для каждой из функций, вывод дан двумя способами. Вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x)
Представлен вывод производных первого порядка арктангенса (arctg x)′ и арккотангенса (arcctg x)′. Для каждой из функций, вывод дан двумя способами. Вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x)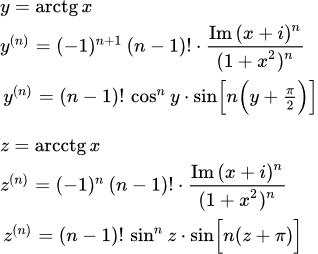 Представлен вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x). Производные даны в двух видах - выраженные через независимую переменную x и через арктангенс (арккотангенс). Вычислены производные от второго до пятого порядка.
Представлен вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x). Производные даны в двух видах - выраженные через независимую переменную x и через арктангенс (арккотангенс). Вычислены производные от второго до пятого порядка.
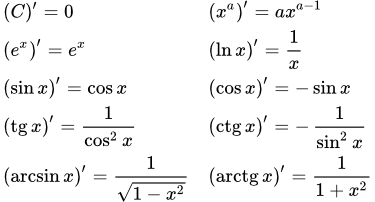 Представлены производные основных элементарных функций и ссылки на страницы с их выводом. Даны формулы производных высших порядков. Производные элементарных функций. Доказательство теоремы
Представлены производные основных элементарных функций и ссылки на страницы с их выводом. Даны формулы производных высших порядков. Производные элементарных функций. Доказательство теоремы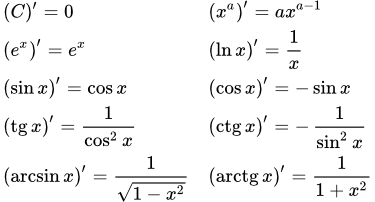 Доказательство теоремы о производных элементарных функций. Доказательство основывается на методах вычисления пределов функций и правилах дифференцирования. Производная натурального логарифма и логарифма по основанию a
Доказательство теоремы о производных элементарных функций. Доказательство основывается на методах вычисления пределов функций и правилах дифференцирования. Производная натурального логарифма и логарифма по основанию a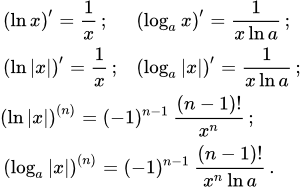 Доказательство и вывод формул производной натурального логарифма и логарифма по основанию a. Примеры вычисления производных от ln 2x, ln 3x и ln nx. Доказательство формулы производной логарифма n-го порядка методом математической индукции. Производная e в степени x и показательной функции
Доказательство и вывод формул производной натурального логарифма и логарифма по основанию a. Примеры вычисления производных от ln 2x, ln 3x и ln nx. Доказательство формулы производной логарифма n-го порядка методом математической индукции. Производная e в степени x и показательной функции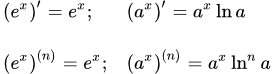 Доказательство и вывод формул производной экспоненты (e в степени x) и показательной функции (a в степени x). Примеры вычисления производных от e^2x, e^3x и e^nx. Формулы производных высших порядков. Производная степенной функции (степени и корни)
Доказательство и вывод формул производной экспоненты (e в степени x) и показательной функции (a в степени x). Примеры вычисления производных от e^2x, e^3x и e^nx. Формулы производных высших порядков. Производная степенной функции (степени и корни)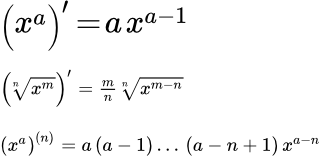 Вывод формулы производной степенной функции (x в степени a). Рассмотрены производные от корней из x. Формула производной степенной функции высшего порядка. Примеры вычисления производных. Производные тригонометрических функций
Вывод формулы производной степенной функции (x в степени a). Рассмотрены производные от корней из x. Формула производной степенной функции высшего порядка. Примеры вычисления производных. Производные тригонометрических функций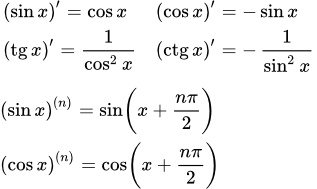 Представлены производные тригонометрических функций. Доказательство и вывод формул. Производные высшего порядка для синуса и косинуса. Производная синуса: (sin x)′
Представлены производные тригонометрических функций. Доказательство и вывод формул. Производные высшего порядка для синуса и косинуса. Производная синуса: (sin x)′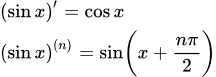 Представлено доказательство и вывод формулы для производной синуса - sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка. Производная косинуса: (cos x)′
Представлено доказательство и вывод формулы для производной синуса - sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка. Производная косинуса: (cos x)′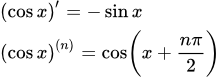 Представлено доказательство и вывод формулы для производной косинуса - cos(x). Примеры вычисления производных от cos 2x, cos 3x, cos nx, косинуса в квадрате, в кубе и в степени n. Формула производной косинуса n-го порядка. Производная тангенса: (tg x)′
Представлено доказательство и вывод формулы для производной косинуса - cos(x). Примеры вычисления производных от cos 2x, cos 3x, cos nx, косинуса в квадрате, в кубе и в степени n. Формула производной косинуса n-го порядка. Производная тангенса: (tg x)′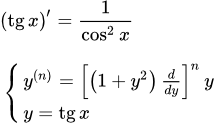 Представлен вывод формулы для производной тангенса - tg(x). Примеры вычисления производных от tg 2x, tg 3x и tg nx. Производная тангенса n-го порядка в виде многочлена по степеням tg(x). Производная котангенса: (ctg x)′
Представлен вывод формулы для производной тангенса - tg(x). Примеры вычисления производных от tg 2x, tg 3x и tg nx. Производная тангенса n-го порядка в виде многочлена по степеням tg(x). Производная котангенса: (ctg x)′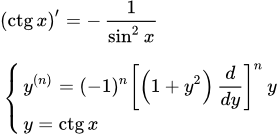 Представлен вывод формулы для производной котангенса - ctg(x). Дана формула производной котангенса n-го порядка в виде многочлена по степеням ctg(x). Коэффициенты этого многочлена связаны рекуррентным соотношением. Вывод производных обратных тригонометрических функций
Представлен вывод формулы для производной котангенса - ctg(x). Дана формула производной котангенса n-го порядка в виде многочлена по степеням ctg(x). Коэффициенты этого многочлена связаны рекуррентным соотношением. Вывод производных обратных тригонометрических функций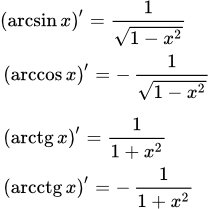 Представлены производные обратных тригонометрических функций и вывод их формул. Также даны выражения производных высших порядков. Ссылки на страницы с более подробным изложением вывода формул. Вывод производных арксинуса (arcsin x)′ и арккосинуса (arccos x)′
Представлены производные обратных тригонометрических функций и вывод их формул. Также даны выражения производных высших порядков. Ссылки на страницы с более подробным изложением вывода формул. Вывод производных арксинуса (arcsin x)′ и арккосинуса (arccos x)′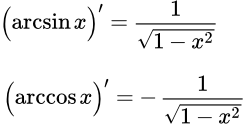 Представлен вывод производных первого порядка арксинуса (arcsin x)′ и арккосинуса (arccos x)′. Для каждой из функций, вывод дан двумя способами. Вывод производных высших порядков арксинуса (arcsin x) и арккосинуса (arccos x)
Представлен вывод производных первого порядка арксинуса (arcsin x)′ и арккосинуса (arccos x)′. Для каждой из функций, вывод дан двумя способами. Вывод производных высших порядков арксинуса (arcsin x) и арккосинуса (arccos x)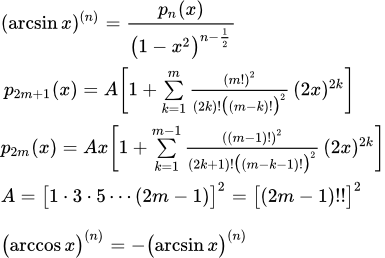 Представлен вывод производных высших порядков арксинуса (arcsin x). Формулы производных арксинуса второго, третьего, четвертого и пятого порядка. Производная n-го порядка выражается через многочлен и корень. Даны уравнения для многочленов и вывод значений их коэффициентов. Выражение производной n-го порядка арккосинуса через производную арксинуса. Вывод производных арктангенса (arctg x)′ и арккотангенса (arcctg x)′
Представлен вывод производных высших порядков арксинуса (arcsin x). Формулы производных арксинуса второго, третьего, четвертого и пятого порядка. Производная n-го порядка выражается через многочлен и корень. Даны уравнения для многочленов и вывод значений их коэффициентов. Выражение производной n-го порядка арккосинуса через производную арксинуса. Вывод производных арктангенса (arctg x)′ и арккотангенса (arcctg x)′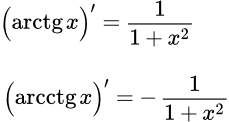 Представлен вывод производных первого порядка арктангенса (arctg x)′ и арккотангенса (arcctg x)′. Для каждой из функций, вывод дан двумя способами. Вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x)
Представлен вывод производных первого порядка арктангенса (arctg x)′ и арккотангенса (arcctg x)′. Для каждой из функций, вывод дан двумя способами. Вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x)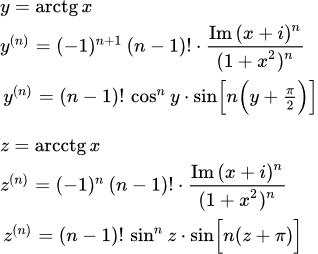 Представлен вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x). Производные даны в двух видах - выраженные через независимую переменную x и через арктангенс (арккотангенс). Вычислены производные от второго до пятого порядка.
Представлен вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x). Производные даны в двух видах - выраженные через независимую переменную x и через арктангенс (арккотангенс). Вычислены производные от второго до пятого порядка. 